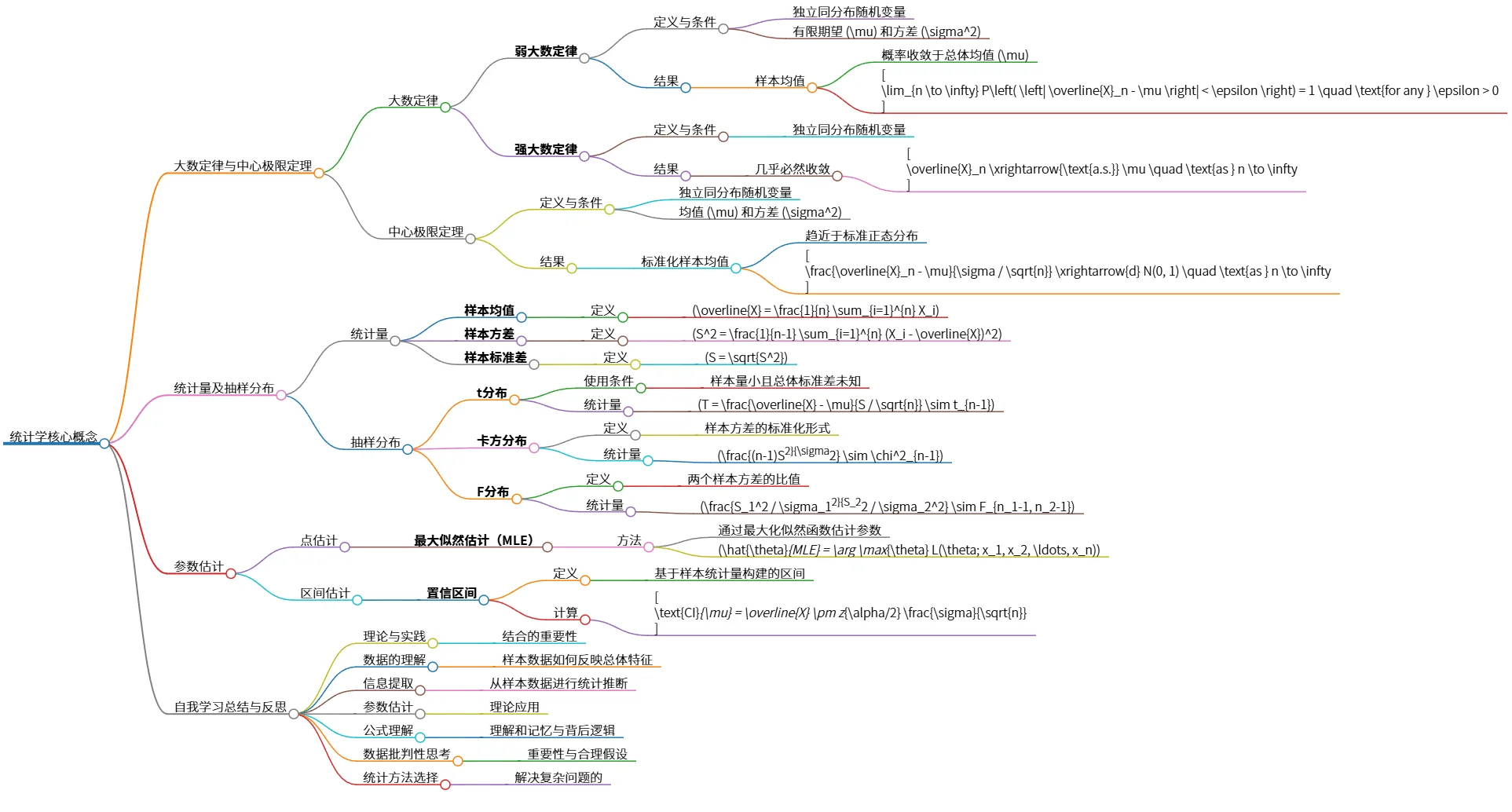
统计学核心概念：大数定律、中心极限定理及参数估计

# 统计学核心概念
## 大数定律与中心极限定理
### 大数定律
- **弱大数定律** 
  - 定义与条件
    - 独立同分布随机变量
    - 有限期望 \(\mu\) 和方差 \(\sigma^2\)
  - 结果
    - 样本均值
      - 概率收敛于总体均值 \(\mu\)
      - \[
      \lim_{n \to \infty} P\left( \left| \overline{X}_n - \mu \right| < \epsilon \right) = 1 \quad \text{for any } \epsilon > 0
      \]
- **强大数定律** 
  - 定义与条件
    - 独立同分布随机变量
  - 结果
    - 几乎必然收敛
      - \[
      \overline{X}_n \xrightarrow{\text{a.s.}} \mu \quad \text{as } n \to \infty
      \]
### 中心极限定理
- 定义与条件
  - 独立同分布随机变量
  - 均值 \(\mu\) 和方差 \(\sigma^2\)
- 结果
  - 标准化样本均值
    - 趋近于标准正态分布
    - \[
    \frac{\overline{X}_n - \mu}{\sigma / \sqrt{n}} \xrightarrow{d} N(0, 1) \quad \text{as } n \to \infty
    \]
## 统计量及抽样分布
### 统计量
- **样本均值** 
  - 定义
    - \(\overline{X} = \frac{1}{n} \sum_{i=1}^{n} X_i\)
- **样本方差** 
  - 定义
    - \(S^2 = \frac{1}{n-1} \sum_{i=1}^{n} (X_i - \overline{X})^2\)
- **样本标准差** 
  - 定义
    - \(S = \sqrt{S^2}\)
### 抽样分布
- **t分布** 
  - 使用条件
    - 样本量小且总体标准差未知
  - 统计量
    - \(T = \frac{\overline{X} - \mu}{S / \sqrt{n}} \sim t_{n-1}\)
- **卡方分布** 
  - 定义
    - 样本方差的标准化形式
  - 统计量
    - \(\frac{(n-1)S^2}{\sigma^2} \sim \chi^2_{n-1}\)
- **F分布** 
  - 定义
    - 两个样本方差的比值
  - 统计量
    - \(\frac{S_1^2 / \sigma_1^2}{S_2^2 / \sigma_2^2} \sim F_{n_1-1, n_2-1}\)
## 参数估计
### 点估计
- **最大似然估计（MLE）** 
  - 方法
    - 通过最大化似然函数估计参数
    - \(\hat{\theta}_{MLE} = \arg \max_{\theta} L(\theta; x_1, x_2, \ldots, x_n)\)
### 区间估计
- **置信区间** 
  - 定义
    - 基于样本统计量构建的区间
  - 计算
    - \[
    \text{CI}_{\mu} = \overline{X} \pm z_{\alpha/2} \frac{\sigma}{\sqrt{n}}
    \]
## 自我学习总结与反思
- 理论与实践
  - 结合的重要性
- 数据的理解
  - 样本数据如何反映总体特征
- 信息提取
  - 从样本数据进行统计推断
- 参数估计
  - 理论应用
- 公式理解
  - 理解和记忆与背后逻辑
- 数据批判性思考
  - 重要性与合理假设
- 统计方法选择
  - 解决复杂问题的