一次函数的定义、性质、图像特征及应用场景解析
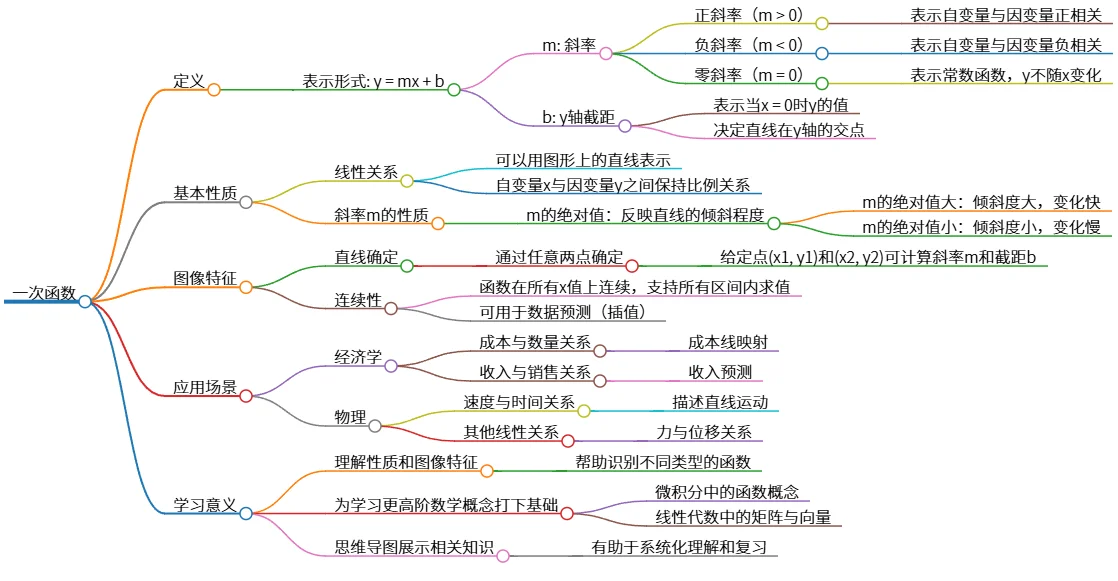
该思维导图概述了一次函数的定义、基本性质、图像特征、应用场景以及学习意义。一次函数以y = mx + b的形式表示,其中m为斜率,b为y轴截距。函数表现出线性关系,斜率的正负影响直线的倾斜方向。图像通过两个点确定,并且具有连续性,适用于经济学和物理等领域。学习一次函数有助于理解相关性质和为更高阶数学概念打下基础。
源码
# 一次函数
## 定义
- 表示形式: y = mx + b
- m: 斜率
- 正斜率(m > 0)
- 表示自变量与因变量正相关
- 负斜率(m < 0)
- 表示自变量与因变量负相关
- 零斜率(m = 0)
- 表示常数函数,y不随x变化
- b: y轴截距
- 表示当x = 0时y的值
- 决定直线在y轴的交点
## 基本性质
- 线性关系
- 可以用图形上的直线表示
- 自变量x与因变量y之间保持比例关系
- 斜率m的性质
- m的绝对值:反映直线的倾斜程度
- m的绝对值大:倾斜度大,变化快
- m的绝对值小:倾斜度小,变化慢
## 图像特征
- 直线确定
- 通过任意两点确定
- 给定点(x1, y1)和(x2, y2)可计算斜率m和截距b
- 连续性
- 函数在所有x值上连续,支持所有区间内求值
- 可用于数据预测(插值)
## 应用场景
- 经济学
- 成本与数量关系
- 成本线映射
- 收入与销售关系
- 收入预测
- 物理
- 速度与时间关系
- 描述直线运动
- 其他线性关系
- 力与位移关系
## 学习意义
- 理解性质和图像特征
- 帮助识别不同类型的函数
- 为学习更高阶数学概念打下基础
- 微积分中的函数概念
- 线性代数中的矩阵与向量
- 思维导图展示相关知识
- 有助于系统化理解和复习
图片