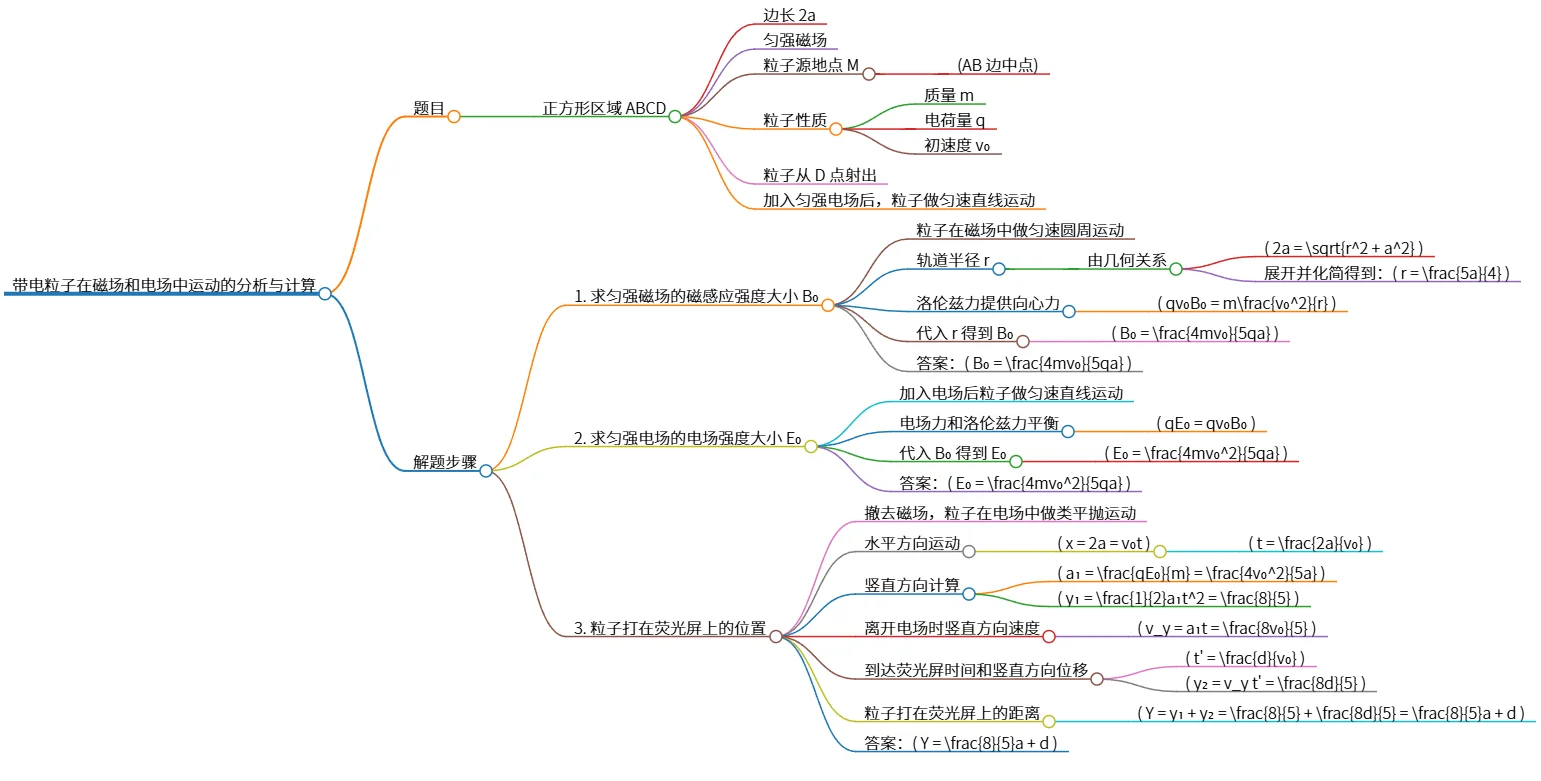
带电粒子在磁场和电场中运动的分析与计算

该思维导图探讨了带电粒子在匀强磁场和电场中的运动。首先计算了粒子在磁场中的磁感应强度 \( B₀ = \frac{4mv₀}{5qa} \) 和电场强度 \( E₀ = \frac{4mv₀^2}{5qa} \)。然后分析了粒子在撤去磁场后进行类平抛运动的过程，得出粒子在荧光屏上的打击位置为 \( Y = \frac{8}{5}a + d \)。整体上，涵盖了粒子在不同场中的动力学行为与计算。

源码

# 带电粒子在磁场和电场中运动的分析与计算
## 题目
- 正方形区域 ABCD
  - 边长 2a
  - 匀强磁场
  - 粒子源地点 M
    - (AB 边中点)
  - 粒子性质
    - 质量 m
    - 电荷量 q
    - 初速度 v₀
  - 粒子从 D 点射出
  - 加入匀强电场后，粒子做匀速直线运动
## 解题步骤
### 1. 求匀强磁场的磁感应强度大小 B₀
- 粒子在磁场中做匀速圆周运动
- 轨道半径 r
  - 由几何关系
    - \( 2a = \sqrt{r^2 + a^2} \)
    - 展开并化简得到：\( r = \frac{5a}{4} \)
- 洛伦兹力提供向心力
  - \( qv₀B₀ = m\frac{v₀^2}{r} \)
- 代入 r 得到 B₀
  - \( B₀ = \frac{4mv₀}{5qa} \)
- 答案：\( B₀ = \frac{4mv₀}{5qa} \)
### 2. 求匀强电场的电场强度大小 E₀
- 加入电场后粒子做匀速直线运动
- 电场力和洛伦兹力平衡
  - \( qE₀ = qv₀B₀ \)
- 代入 B₀ 得到 E₀
  - \( E₀ = \frac{4mv₀^2}{5qa} \)
- 答案：\( E₀ = \frac{4mv₀^2}{5qa} \)
### 3. 粒子打在荧光屏上的位置
- 撤去磁场，粒子在电场中做类平抛运动
- 水平方向运动
  - \( x = 2a = v₀t \)
    - \( t = \frac{2a}{v₀} \)
- 竖直方向计算
  - \( a₁ = \frac{qE₀}{m} = \frac{4v₀^2}{5a} \)
  - \( y₁ = \frac{1}{2}a₁t^2 = \frac{8}{5} \)
- 离开电场时竖直方向速度
  - \( v_y = a₁t = \frac{8v₀}{5} \)
- 到达荧光屏时间和竖直方向位移
  - \( t' = \frac{d}{v₀} \)
  - \( y₂ = v_y t' = \frac{8d}{5} \)
- 粒子打在荧光屏上的距离
  - \( Y = y₁ + y₂ = \frac{8}{5} + \frac{8d}{5} = \frac{8}{5}a + d \)
- 答案：\( Y = \frac{8}{5}a + d \)

图片