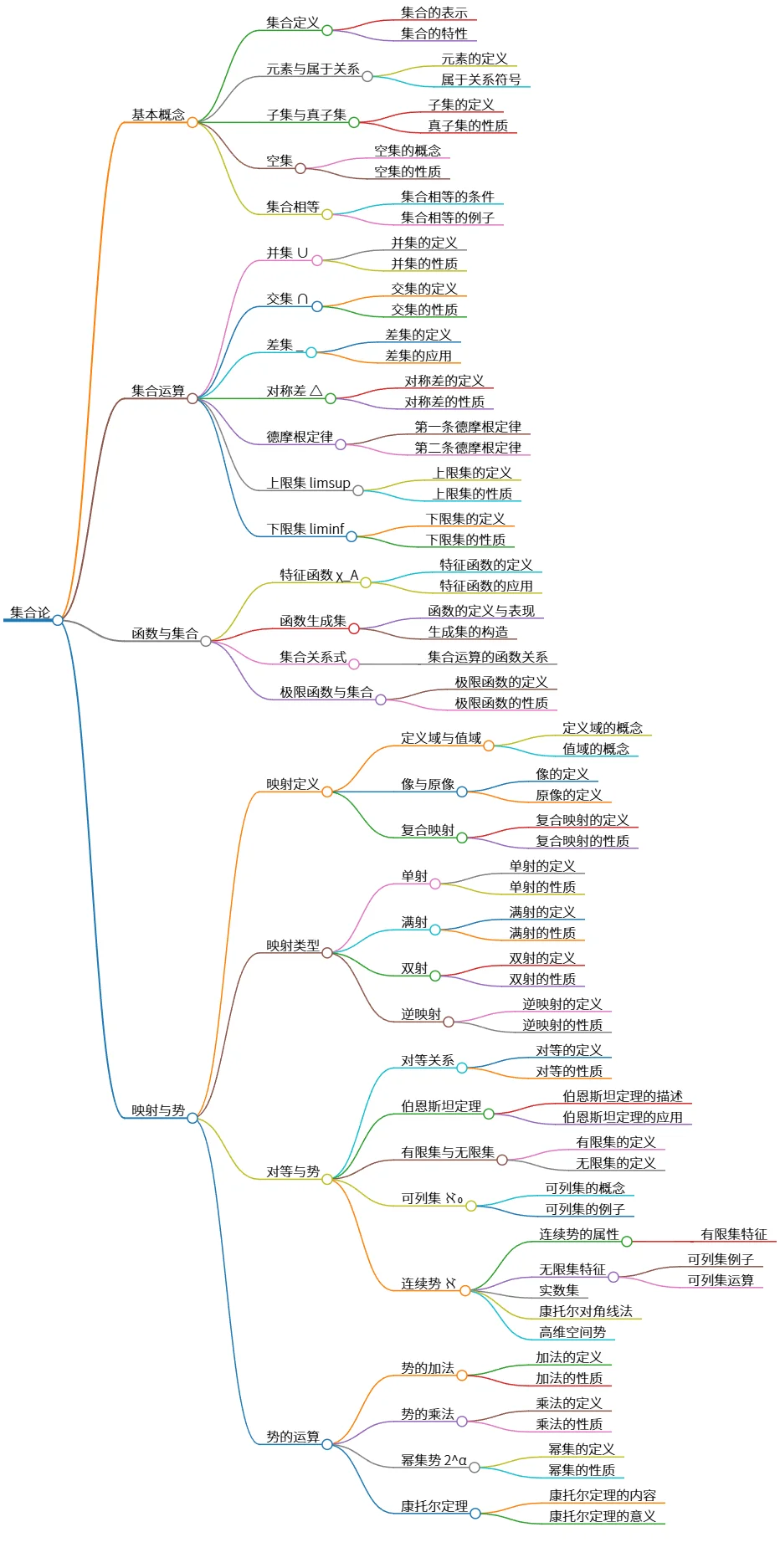
集合论的基本概念、运算及映射与势的关系

# 集合论
## 基本概念
### 集合定义
#### 集合的表示
#### 集合的特性
### 元素与属于关系
#### 元素的定义
#### 属于关系符号
### 子集与真子集
#### 子集的定义
#### 真子集的性质
### 空集
#### 空集的概念
#### 空集的性质
### 集合相等
#### 集合相等的条件
#### 集合相等的例子
## 集合运算
### 并集 ∪
#### 并集的定义
#### 并集的性质
### 交集 ∩
#### 交集的定义
#### 交集的性质
### 差集 _
#### 差集的定义
#### 差集的应用
### 对称差 △
#### 对称差的定义
#### 对称差的性质
### 德摩根定律
#### 第一条德摩根定律
#### 第二条德摩根定律
### 上限集 limsup
#### 上限集的定义
#### 上限集的性质
### 下限集 liminf
#### 下限集的定义
#### 下限集的性质
## 函数与集合
### 特征函数 χ_A
#### 特征函数的定义
#### 特征函数的应用
### 函数生成集
#### 函数的定义与表现
#### 生成集的构造
### 集合关系式
#### 集合运算的函数关系
### 极限函数与集合
#### 极限函数的定义
#### 极限函数的性质
## 映射与势
### 映射定义
#### 定义域与值域
##### 定义域的概念 
##### 值域的概念 
#### 像与原像
##### 像的定义
##### 原像的定义
#### 复合映射
##### 复合映射的定义
##### 复合映射的性质
### 映射类型
#### 单射
##### 单射的定义
##### 单射的性质
#### 满射
##### 满射的定义
##### 满射的性质
#### 双射
##### 双射的定义
##### 双射的性质
#### 逆映射
##### 逆映射的定义
##### 逆映射的性质
### 对等与势
#### 对等关系
##### 对等的定义
##### 对等的性质
#### 伯恩斯坦定理
##### 伯恩斯坦定理的描述
##### 伯恩斯坦定理的应用
#### 有限集与无限集
##### 有限集的定义
##### 无限集的定义
#### 可列集 ℵ₀
##### 可列集的概念
##### 可列集的例子
#### 连续势 ℵ
##### 连续势的属性
###### 有限集特征
##### 无限集特征
###### 可列集例子
###### 可列集运算
##### 实数集
##### 康托尔对角线法
##### 高维空间势
### 势的运算
#### 势的加法
##### 加法的定义
##### 加法的性质
#### 势的乘法
##### 乘法的定义
##### 乘法的性质
#### 幂集势 2^α
##### 幂集的定义
##### 幂集的性质
#### 康托尔定理
##### 康托尔定理的内容
##### 康托尔定理的意义