粒子运动分析:速度、电势、周期及最远距离解析
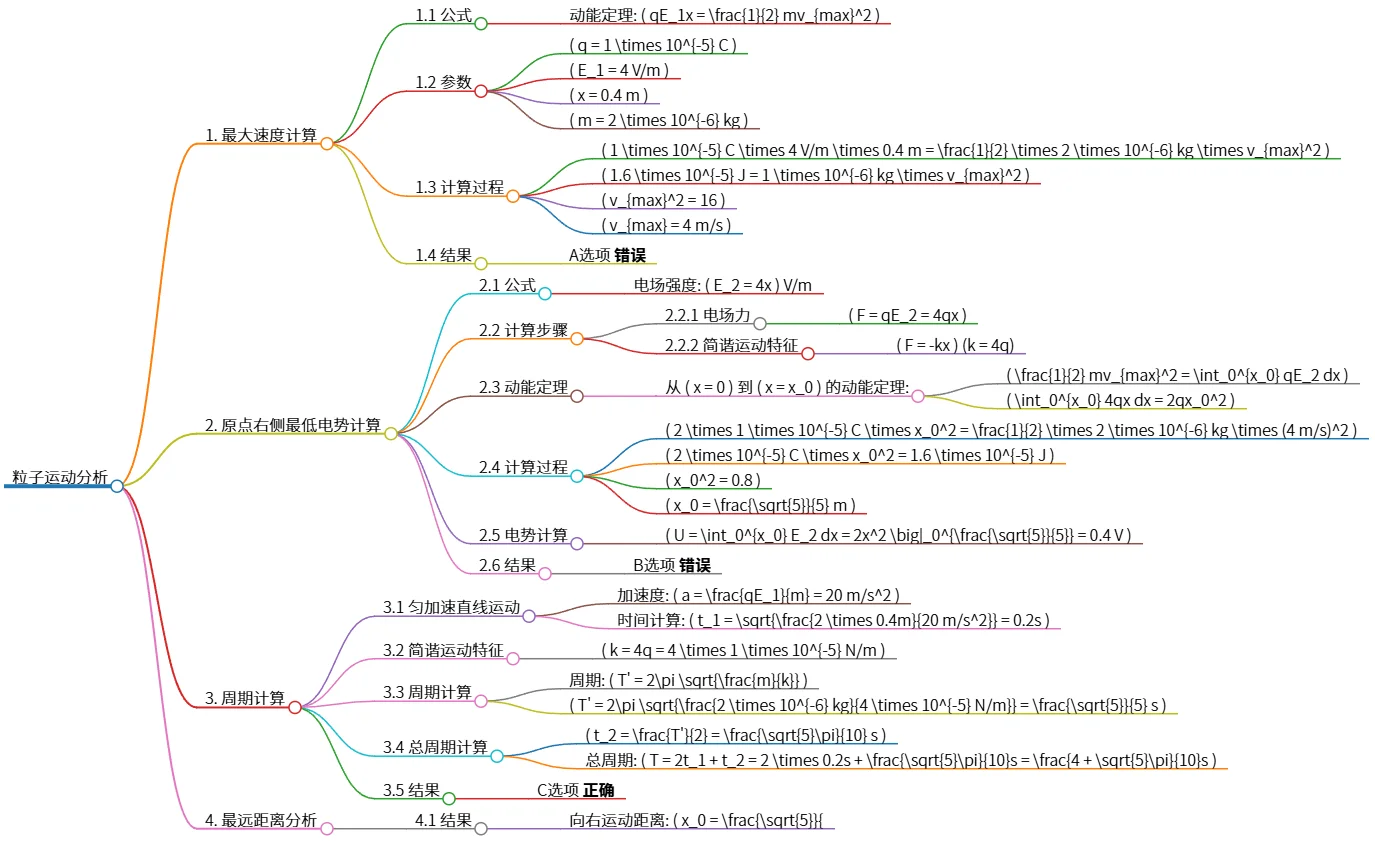
该思维导图分析了粒子运动的相关问题,包括最大速度计算、原点右侧最低电势、周期计算及最远距离分析。通过动能定理和电场强度的公式,得出了粒子的最大速度为4 m/s,电势为0.4 V,周期计算结果为 \(T = \frac{4 + \sqrt{5}\pi}{10}s\)。最终,选项C和D为正确答案,展示了粒子在电场中的运动特征和行为。
源码
# 粒子运动分析
## 1. 最大速度计算
### 1.1 公式
- 动能定理: \( qE_1x = \frac{1}{2} mv_{max}^2 \)
### 1.2 参数
- \( q = 1 \times 10^{-5} C \)
- \( E_1 = 4 V/m \)
- \( x = 0.4 m \)
- \( m = 2 \times 10^{-6} kg \)
### 1.3 计算过程
- \( 1 \times 10^{-5} C \times 4 V/m \times 0.4 m = \frac{1}{2} \times 2 \times 10^{-6} kg \times v_{max}^2 \)
- \( 1.6 \times 10^{-5} J = 1 \times 10^{-6} kg \times v_{max}^2 \)
- \( v_{max}^2 = 16 \)
- \( v_{max} = 4 m/s \)
### 1.4 结果
- A选项 **错误**
## 2. 原点右侧最低电势计算
### 2.1 公式
- 电场强度: \( E_2 = 4x \) V/m
### 2.2 计算步骤
#### 2.2.1 电场力
- \( F = qE_2 = 4qx \)
#### 2.2.2 简谐运动特征
- \( F = -kx \) (k = 4q)
### 2.3 动能定理
- 从 \( x = 0 \) 到 \( x = x_0 \) 的动能定理:
- \( \frac{1}{2} mv_{max}^2 = \int_0^{x_0} qE_2 dx \)
- \( \int_0^{x_0} 4qx dx = 2qx_0^2 \)
### 2.4 计算过程
- \( 2 \times 1 \times 10^{-5} C \times x_0^2 = \frac{1}{2} \times 2 \times 10^{-6} kg \times (4 m/s)^2 \)
- \( 2 \times 10^{-5} C \times x_0^2 = 1.6 \times 10^{-5} J \)
- \( x_0^2 = 0.8 \)
- \( x_0 = \frac{\sqrt{5}}{5} m \)
### 2.5 电势计算
- \( U = \int_0^{x_0} E_2 dx = 2x^2 \big|_0^{\frac{\sqrt{5}}{5}} = 0.4 V \)
### 2.6 结果
- B选项 **错误**
## 3. 周期计算
### 3.1 匀加速直线运动
- 加速度: \( a = \frac{qE_1}{m} = 20 m/s^2 \)
- 时间计算: \( t_1 = \sqrt{\frac{2 \times 0.4m}{20 m/s^2}} = 0.2s \)
### 3.2 简谐运动特征
- \( k = 4q = 4 \times 1 \times 10^{-5} N/m \)
### 3.3 周期计算
- 周期: \( T' = 2\pi \sqrt{\frac{m}{k}} \)
- \( T' = 2\pi \sqrt{\frac{2 \times 10^{-6} kg}{4 \times 10^{-5} N/m}} = \frac{\sqrt{5}}{5} s \)
### 3.4 总周期计算
- \( t_2 = \frac{T'}{2} = \frac{\sqrt{5}\pi}{10} s \)
- 总周期: \( T = 2t_1 + t_2 = 2 \times 0.2s + \frac{\sqrt{5}\pi}{10}s = \frac{4 + \sqrt{5}\pi}{10}s \)
### 3.5 结果
- C选项 **正确**
## 4. 最远距离分析
### 4.1 结果
- 向右运动距离: \( x_0 = \frac{\sqrt{5}}{
图片