函数分析:对单调性与极值点的充分必要条件研究
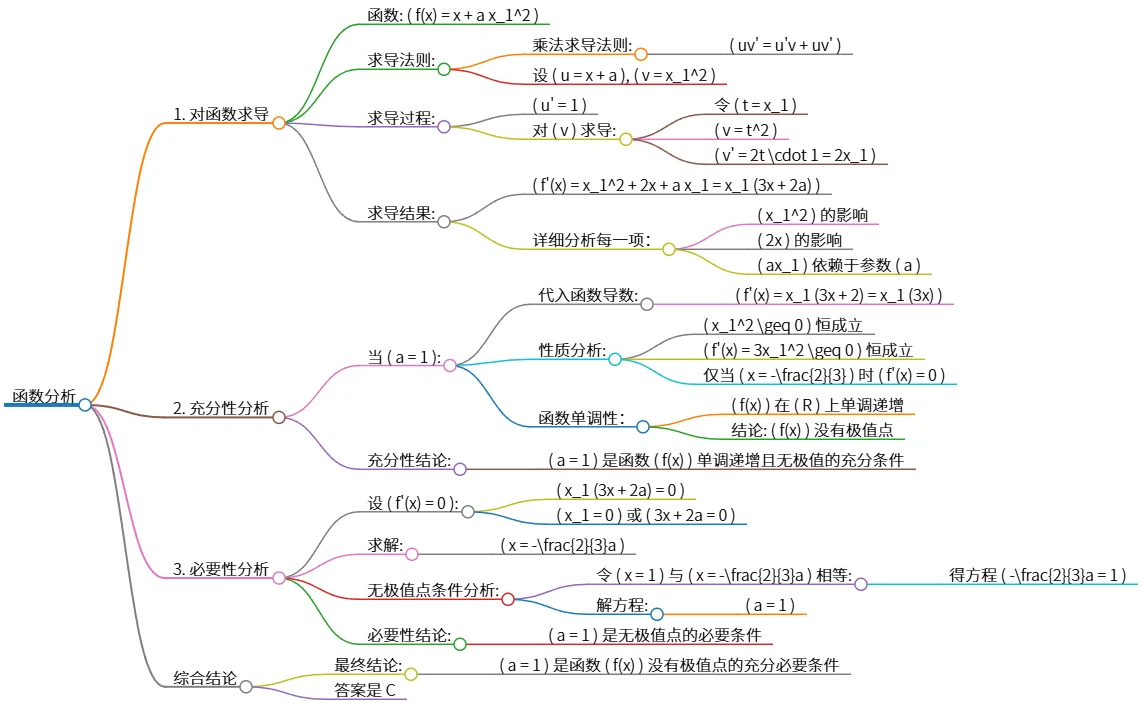
该思维导图分析了函数 \( f(x) = x + a x_1^2 \) 的导数及其单调性。首先通过求导得到 \( f'(x) = x_1 (3x + 2a) \)。当 \( a = 1 \) 时,函数单调递增且无极值点。必要性分析表明,当 \( f'(x) = 0 \) 时,\( a = 1 \) 是无极值点的充分必要条件。因此,结论为 \( a = 1 \) 是函数 \( f(x) \) 没有极值点的唯一条件。最终答案为 C。
源码
# 函数分析
## 1. 对函数求导
- 函数: \( f(x) = x + a x_1^2 \)
- 求导法则:
- 乘法求导法则:
- \( uv' = u'v + uv' \)
- 设 \( u = x + a \), \( v = x_1^2 \)
- 求导过程:
- \( u' = 1 \)
- 对 \( v \) 求导:
- 令 \( t = x_1 \)
- \( v = t^2 \)
- \( v' = 2t \cdot 1 = 2x_1 \)
- 求导结果:
- \( f'(x) = x_1^2 + 2x + a x_1 = x_1 (3x + 2a) \)
- 详细分析每一项:
- \( x_1^2 \) 的影响
- \( 2x \) 的影响
- \( ax_1 \) 依赖于参数 \( a \)
## 2. 充分性分析
- 当 \( a = 1 \):
- 代入函数导数:
- \( f'(x) = x_1 (3x + 2) = x_1 (3x) \)
- 性质分析:
- \( x_1^2 \geq 0 \) 恒成立
- \( f'(x) = 3x_1^2 \geq 0 \) 恒成立
- 仅当 \( x = -\frac{2}{3} \) 时 \( f'(x) = 0 \)
- 函数单调性:
- \( f(x) \) 在 \( R \) 上单调递增
- 结论: \( f(x) \) 没有极值点
- 充分性结论:
- \( a = 1 \) 是函数 \( f(x) \) 单调递增且无极值的充分条件
## 3. 必要性分析
- 设 \( f'(x) = 0 \):
- \( x_1 (3x + 2a) = 0 \)
- \( x_1 = 0 \) 或 \( 3x + 2a = 0 \)
- 求解:
- \( x = -\frac{2}{3}a \)
- 无极值点条件分析:
- 令 \( x = 1 \) 与 \( x = -\frac{2}{3}a \) 相等:
- 得方程 \( -\frac{2}{3}a = 1 \)
- 解方程:
- \( a = 1 \)
- 必要性结论:
- \( a = 1 \) 是无极值点的必要条件
## 综合结论
- 最终结论:
- \( a = 1 \) 是函数 \( f(x) \) 没有极值点的充分必要条件
- 答案是 C
图片