数列极限与函数极限的关系与基本概念分析
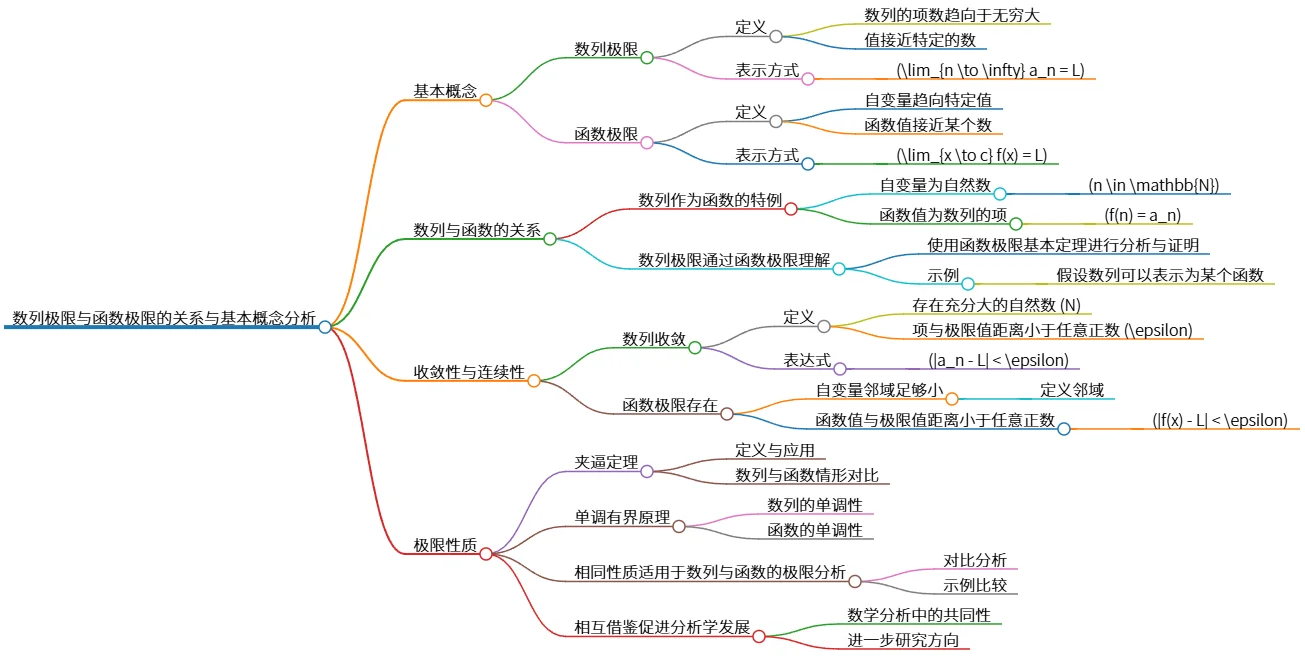
该思维导图探讨了数列极限与函数极限的联系,首先定义了数列与函数极限的基本概念,指出数列可视为函数的特例,并使用函数极限理论分析数列极限。接着讨论了数列的收敛和函数的连续性,强调了极限的夹逼定理和单调有界原理等性质,这些相同的性质用于数列和函数的极限分析,促进了分析学的发展。
源码
# 数列极限与函数极限的关系与基本概念分析
## 基本概念
- 数列极限
- 定义
- 数列的项数趋向于无穷大
- 值接近特定的数
- 表示方式
- \(\lim_{n \to \infty} a_n = L\)
- 函数极限
- 定义
- 自变量趋向特定值
- 函数值接近某个数
- 表示方式
- \(\lim_{x \to c} f(x) = L\)
## 数列与函数的关系
- 数列作为函数的特例
- 自变量为自然数
- \(n \in \mathbb{N}\)
- 函数值为数列的项
- \(f(n) = a_n\)
- 数列极限通过函数极限理解
- 使用函数极限基本定理进行分析与证明
- 示例
- 假设数列可以表示为某个函数
## 收敛性与连续性
- 数列收敛
- 定义
- 存在充分大的自然数 \(N\)
- 项与极限值距离小于任意正数 \(\epsilon\)
- 表达式
- \(|a_n - L| < \epsilon\)
- 函数极限存在
- 自变量邻域足够小
- 定义邻域
- 函数值与极限值距离小于任意正数
- \(|f(x) - L| < \epsilon\)
## 极限性质
- 夹逼定理
- 定义与应用
- 数列与函数情形对比
- 单调有界原理
- 数列的单调性
- 函数的单调性
- 相同性质适用于数列与函数的极限分析
- 对比分析
- 示例比较
- 相互借鉴促进分析学发展
- 数学分析中的共同性
- 进一步研究方向
图片