极限与连续、一元函数微分学知识体系解析与应用
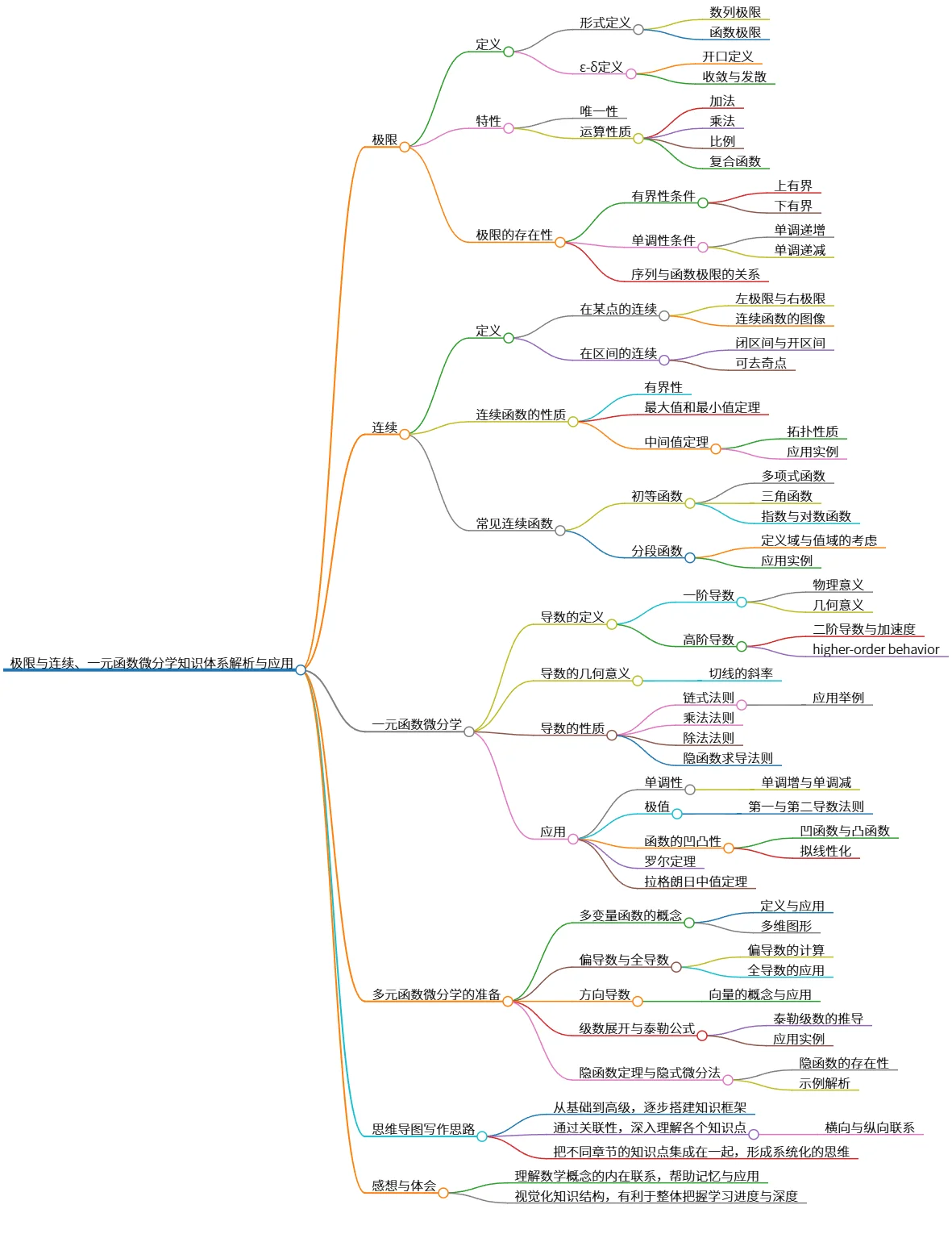
该思维导图涵盖了极限与连续、一元函数微分学的主要概念,包含极限的定义、特性和存在性,连续函数的性质及常见类型,以及导数的定义、几何意义和应用。此外,还介绍了多元函数微分学的基础知识和思维导图的写作思路,强调通过系统化的结构便于理解和记忆数学概念,有助于学习的整体把握。
源码
# 极限与连续、一元函数微分学知识体系解析与应用
## 极限
- 定义
- 形式定义
- 数列极限
- 函数极限
- ε-δ定义
- 开口定义
- 收敛与发散
- 特性
- 唯一性
- 运算性质
- 加法
- 乘法
- 比例
- 复合函数
- 极限的存在性
- 有界性条件
- 上有界
- 下有界
- 单调性条件
- 单调递增
- 单调递减
- 序列与函数极限的关系
## 连续
- 定义
- 在某点的连续
- 左极限与右极限
- 连续函数的图像
- 在区间的连续
- 闭区间与开区间
- 可去奇点
- 连续函数的性质
- 有界性
- 最大值和最小值定理
- 中间值定理
- 拓扑性质
- 应用实例
- 常见连续函数
- 初等函数
- 多项式函数
- 三角函数
- 指数与对数函数
- 分段函数
- 定义域与值域的考虑
- 应用实例
## 一元函数微分学
- 导数的定义
- 一阶导数
- 物理意义
- 几何意义
- 高阶导数
- 二阶导数与加速度
- higher-order behavior
- 导数的几何意义
- 切线的斜率
- 导数的性质
- 链式法则
- 应用举例
- 乘法法则
- 除法法则
- 隐函数求导法则
- 应用
- 单调性
- 单调增与单调减
- 极值
- 第一与第二导数法则
- 函数的凹凸性
- 凹函数与凸函数
- 拟线性化
- 罗尔定理
- 拉格朗日中值定理
## 多元函数微分学的准备
- 多变量函数的概念
- 定义与应用
- 多维图形
- 偏导数与全导数
- 偏导数的计算
- 全导数的应用
- 方向导数
- 向量的概念与应用
- 级数展开与泰勒公式
- 泰勒级数的推导
- 应用实例
- 隐函数定理与隐式微分法
- 隐函数的存在性
- 示例解析
## 思维导图写作思路
- 从基础到高级,逐步搭建知识框架
- 通过关联性,深入理解各个知识点
- 横向与纵向联系
- 把不同章节的知识点集成在一起,形成系统化的思维
## 感想与体会
- 理解数学概念的内在联系,帮助记忆与应用
- 视觉化知识结构,有利于整体把握学习进度与深度
图片