流体静力学核心知识体系与受力计算解析
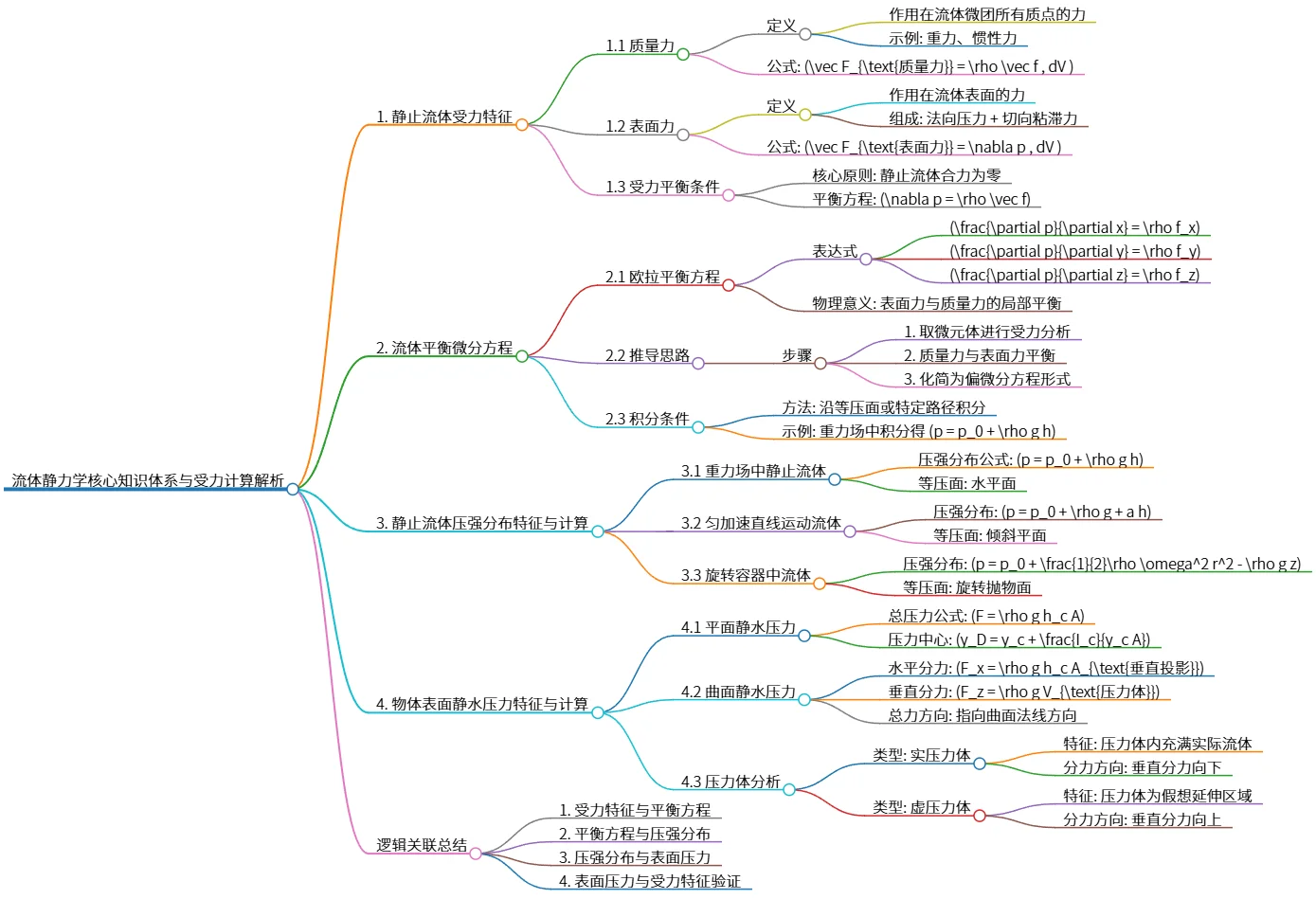
该思维导图系统地阐述了流体静力学的核心知识体系,包括静止流体的受力特征(质量力与表面力)、流体平衡微分方程(欧拉平衡方程及其推导)、静止流体的压强分布特征(在重力场、匀加速运动与旋转容器中的压强分布)、以及物体表面的静水压力计算(平面与曲面静水压力及压力体分析)。通过逻辑关联,总结了受力、平衡与压强之间的关系,为流体静力学的理解提供了清晰的框架。
源码
# 流体静力学核心知识体系与受力计算解析
## 1. 静止流体受力特征
### 1.1 质量力
- 定义
- 作用在流体微团所有质点的力
- 示例: 重力、惯性力
- 公式: \(\vec F_{\text{质量力}} = \rho \vec f \, dV \)
### 1.2 表面力
- 定义
- 作用在流体表面的力
- 组成: 法向压力 + 切向粘滞力
- 公式: \(\vec F_{\text{表面力}} = \nabla p \, dV \)
### 1.3 受力平衡条件
- 核心原则: 静止流体合力为零
- 平衡方程: \(\nabla p = \rho \vec f\)
## 2. 流体平衡微分方程
### 2.1 欧拉平衡方程
- 表达式
- \(\frac{\partial p}{\partial x} = \rho f_x\)
- \(\frac{\partial p}{\partial y} = \rho f_y\)
- \(\frac{\partial p}{\partial z} = \rho f_z\)
- 物理意义: 表面力与质量力的局部平衡
### 2.2 推导思路
- 步骤
1. 取微元体进行受力分析
2. 质量力与表面力平衡
3. 化简为偏微分方程形式
### 2.3 积分条件
- 方法: 沿等压面或特定路径积分
- 示例: 重力场中积分得 \(p = p_0 + \rho g h\)
## 3. 静止流体压强分布特征与计算
### 3.1 重力场中静止流体
- 压强分布公式: \(p = p_0 + \rho g h\)
- 等压面: 水平面
### 3.2 匀加速直线运动流体
- 压强分布: \(p = p_0 + \rho g + a h\)
- 等压面: 倾斜平面
### 3.3 旋转容器中流体
- 压强分布: \(p = p_0 + \frac{1}{2}\rho \omega^2 r^2 - \rho g z\)
- 等压面: 旋转抛物面
## 4. 物体表面静水压力特征与计算
### 4.1 平面静水压力
- 总压力公式: \(F = \rho g h_c A\)
- 压力中心: \(y_D = y_c + \frac{I_c}{y_c A}\)
### 4.2 曲面静水压力
- 水平分力: \(F_x = \rho g h_c A_{\text{垂直投影}}\)
- 垂直分力: \(F_z = \rho g V_{\text{压力体}}\)
- 总力方向: 指向曲面法线方向
### 4.3 压力体分析
- 类型: 实压力体
- 特征: 压力体内充满实际流体
- 分力方向: 垂直分力向下
- 类型: 虚压力体
- 特征: 压力体为假想延伸区域
- 分力方向: 垂直分力向上
## 逻辑关联总结
### 1. 受力特征与平衡方程
### 2. 平衡方程与压强分布
### 3. 压强分布与表面压力
### 4. 表面压力与受力特征验证
图片