矢量的基本概念、运算、分解及其应用探讨
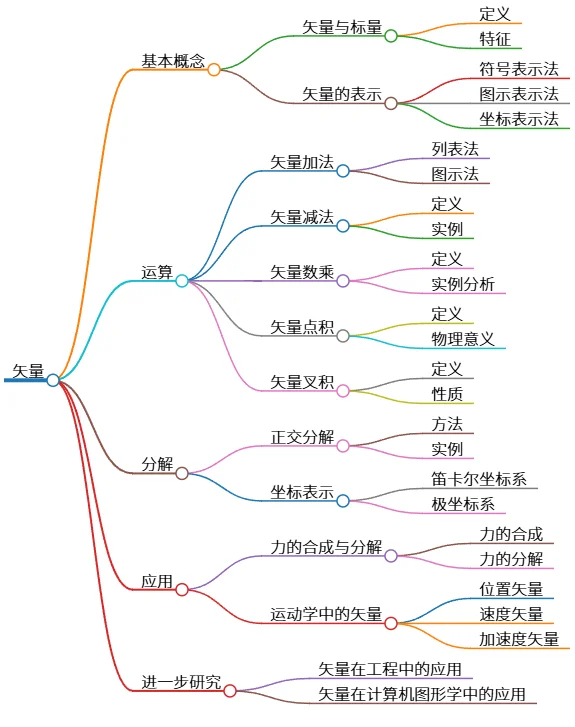
该思维导图涵盖了矢量的基本概念、运算、分解及应用等方面。基本概念部分介绍了矢量与标量的区别和矢量的表示方法。运算部分包括矢量加法、减法、数乘、点积和叉积。分解部分讨论了正交分解和坐标表示。最后,应用部分阐述了力的合成与分解及运动学中的矢量应用,展示了矢量在物理学中的重要性。
源码
# 矢量
## 基本概念
### 矢量与标量
#### 定义
#### 特征
### 矢量的表示
#### 符号表示法
#### 图示表示法
#### 坐标表示法
## 运算
### 矢量加法
#### 列表法
#### 图示法
### 矢量减法
#### 定义
#### 实例
### 矢量数乘
#### 定义
#### 实例分析
### 矢量点积
#### 定义
#### 物理意义
### 矢量叉积
#### 定义
#### 性质
## 分解
### 正交分解
#### 方法
#### 实例
### 坐标表示
#### 笛卡尔坐标系
#### 极坐标系
## 应用
### 力的合成与分解
#### 力的合成
#### 力的分解
### 运动学中的矢量
#### 位置矢量
#### 速度矢量
#### 加速度矢量
## 进一步研究
### 矢量在工程中的应用
### 矢量在计算机图形学中的应用
图片