函数与极限的基本概念、性质及应用探讨
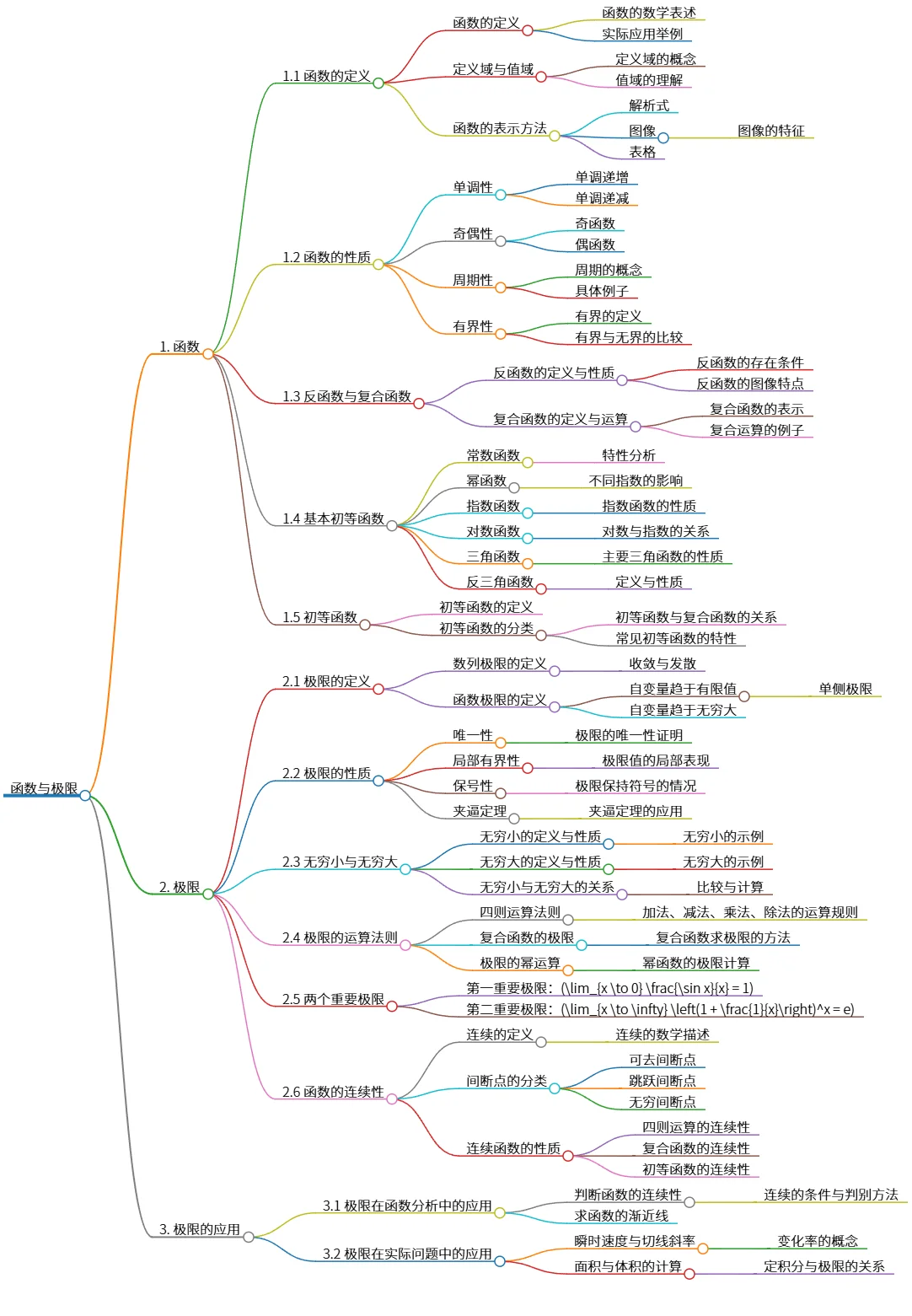
该思维导图包括函数与极限的基本概念。首先介绍了函数的定义、性质、反函数与复合函数,涵盖基本初等函数与初等函数的分类。接着,讲解极限的定义、性质、无穷小与无穷大、极限的运算法则及重要极限,最后探讨函数的连续性及间断点的分类。极限的应用部分涉及函数分析中的连续性判断及渐近线求解,以及在实际问题中的应用,如瞬时速度和面积与体积的计算。
源码
# 函数与极限
## 1. 函数
### 1.1 函数的定义
- 函数的定义
- 函数的数学表述
- 实际应用举例
- 定义域与值域
- 定义域的概念
- 值域的理解
- 函数的表示方法
- 解析式
- 图像
- 图像的特征
- 表格
### 1.2 函数的性质
- 单调性
- 单调递增
- 单调递减
- 奇偶性
- 奇函数
- 偶函数
- 周期性
- 周期的概念
- 具体例子
- 有界性
- 有界的定义
- 有界与无界的比较
### 1.3 反函数与复合函数
- 反函数的定义与性质
- 反函数的存在条件
- 反函数的图像特点
- 复合函数的定义与运算
- 复合函数的表示
- 复合运算的例子
### 1.4 基本初等函数
- 常数函数
- 特性分析
- 幂函数
- 不同指数的影响
- 指数函数
- 指数函数的性质
- 对数函数
- 对数与指数的关系
- 三角函数
- 主要三角函数的性质
- 反三角函数
- 定义与性质
### 1.5 初等函数
- 初等函数的定义
- 初等函数的分类
- 初等函数与复合函数的关系
- 常见初等函数的特性
## 2. 极限
### 2.1 极限的定义
- 数列极限的定义
- 收敛与发散
- 函数极限的定义
- 自变量趋于有限值
- 单侧极限
- 自变量趋于无穷大
### 2.2 极限的性质
- 唯一性
- 极限的唯一性证明
- 局部有界性
- 极限值的局部表现
- 保号性
- 极限保持符号的情况
- 夹逼定理
- 夹逼定理的应用
### 2.3 无穷小与无穷大
- 无穷小的定义与性质
- 无穷小的示例
- 无穷大的定义与性质
- 无穷大的示例
- 无穷小与无穷大的关系
- 比较与计算
### 2.4 极限的运算法则
- 四则运算法则
- 加法、减法、乘法、除法的运算规则
- 复合函数的极限
- 复合函数求极限的方法
- 极限的幂运算
- 幂函数的极限计算
### 2.5 两个重要极限
- 第一重要极限:\(\lim_{x \to 0} \frac{\sin x}{x} = 1\)
- 第二重要极限:\(\lim_{x \to \infty} \left(1 + \frac{1}{x}\right)^x = e\)
### 2.6 函数的连续性
- 连续的定义
- 连续的数学描述
- 间断点的分类
- 可去间断点
- 跳跃间断点
- 无穷间断点
- 连续函数的性质
- 四则运算的连续性
- 复合函数的连续性
- 初等函数的连续性
## 3. 极限的应用
### 3.1 极限在函数分析中的应用
- 判断函数的连续性
- 连续的条件与判别方法
- 求函数的渐近线
### 3.2 极限在实际问题中的应用
- 瞬时速度与切线斜率
- 变化率的概念
- 面积与体积的计算
- 定积分与极限的关系
图片