集合与函数：函数的基本概念及其性质详细解析

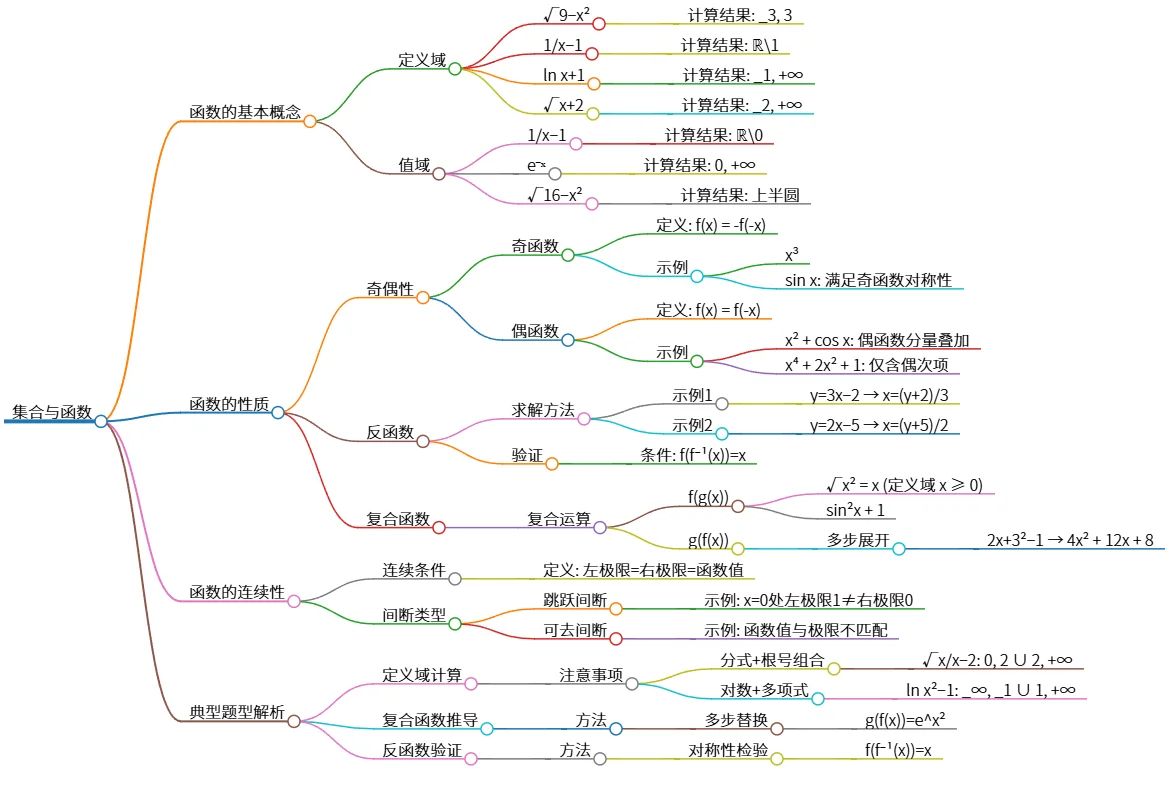
# 集合与函数
## 函数的基本概念
### 定义域
- √9−x²
  - 计算结果: _3, 3
- 1/x−1
  - 计算结果: ℝ\\1
- ln x+1
  - 计算结果: _1, +∞
- √x+2
  - 计算结果: _2, +∞
### 值域
- 1/x−1
  - 计算结果: ℝ\\0
- e⁻ˣ
  - 计算结果: 0, +∞
- √16−x²
  - 计算结果: 上半圆
## 函数的性质
### 奇偶性
#### 奇函数
- 定义: f(x) = -f(-x)
- 示例
  - x³
  - sin x: 满足奇函数对称性
#### 偶函数
- 定义: f(x) = f(-x)
- 示例
  - x² + cos x: 偶函数分量叠加
  - x⁴ + 2x² + 1: 仅含偶次项
### 反函数
#### 求解方法
- 示例1
  - y=3x−2 → x=(y+2)/3
- 示例2
  - y=2x−5 → x=(y+5)/2
#### 验证
- 条件: f(f⁻¹(x))=x
### 复合函数
#### 复合运算
- f(g(x))
  - √x² = x (定义域 x ≥ 0)
  - sin²x + 1
- g(f(x))
  - 多步展开
    - 2x+3²−1 → 4x² + 12x + 8
## 函数的连续性
### 连续条件
- 定义: 左极限=右极限=函数值
### 间断类型
- 跳跃间断
  - 示例: x=0处左极限1≠右极限0
- 可去间断
  - 示例: 函数值与极限不匹配
## 典型题型解析
### 定义域计算
- 注意事项
  - 分式+根号组合
    - √x/x−2: 0, 2 ∪ 2, +∞
  - 对数+多项式
    - ln x²−1: _∞, _1 ∪ 1, +∞
### 复合函数推导
- 方法
  - 多步替换
    - g(f(x))=e^x²
### 反函数验证
- 方法
  - 对称性检验
    - f(f⁻¹(x))=x