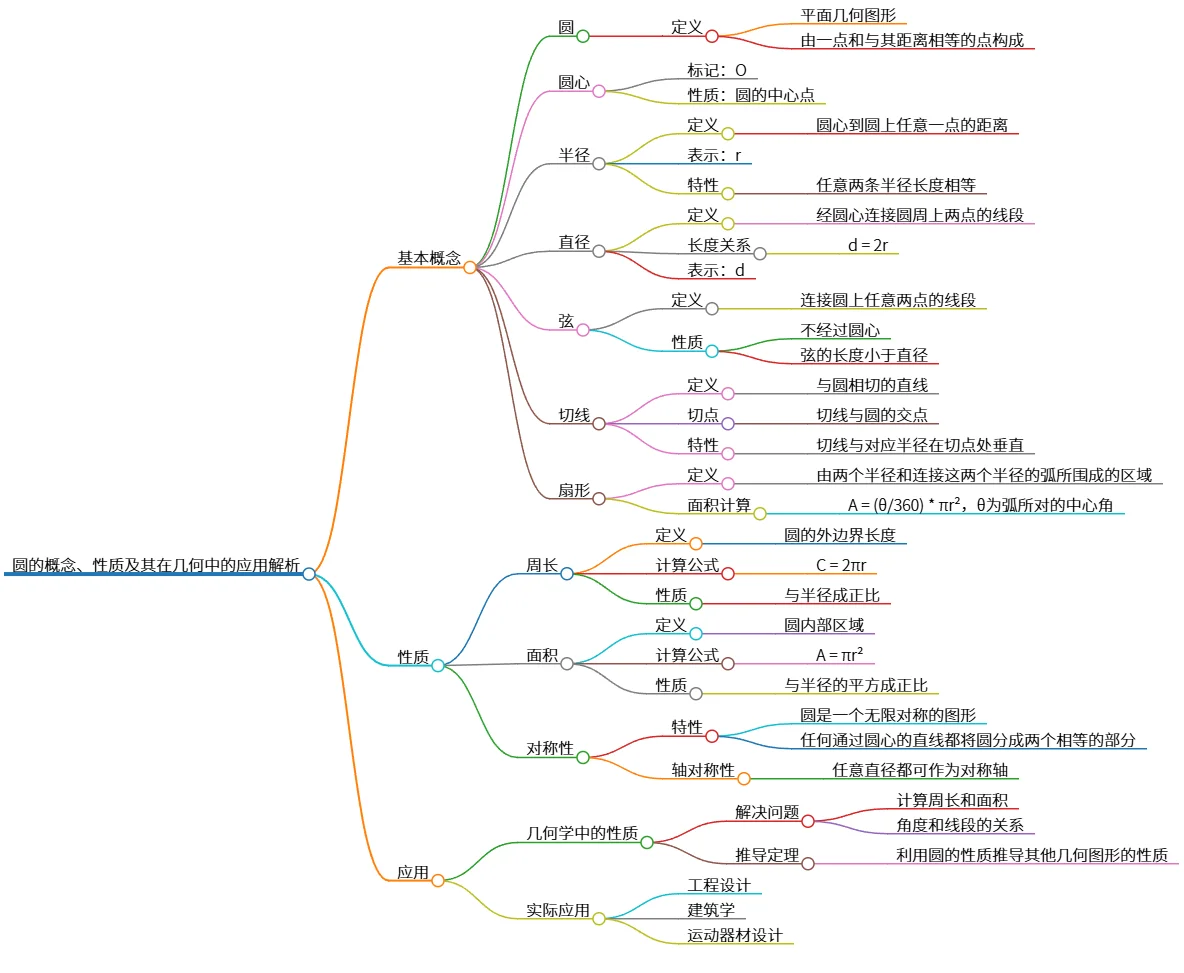
圆的概念、性质及其在几何中的应用解析

该思维导图概述了圆的基本概念和性质，包括定义、圆心、半径、直径、弦、切线和扇形等基本元素。还介绍了圆的周长和面积的计算公式，以及其对称性特征。圆在几何学中具有重要应用，能够帮助理解平面几何题目，并推导和证明其他几何形状的性质。

源码

# 圆的概念、性质及其在几何中的应用解析
## 基本概念
- 圆
  - 定义
    - 平面几何图形
    - 由一点和与其距离相等的点构成
- 圆心
  - 标记：O
  - 性质：圆的中心点
- 半径
  - 定义
    - 圆心到圆上任意一点的距离
  - 表示：r
  - 特性
    - 任意两条半径长度相等
- 直径
  - 定义
    - 经圆心连接圆周上两点的线段
  - 长度关系
    - d = 2r
  - 表示：d
- 弦
  - 定义
    - 连接圆上任意两点的线段
  - 性质
    - 不经过圆心
    - 弦的长度小于直径
- 切线
  - 定义
    - 与圆相切的直线
  - 切点
    - 切线与圆的交点
  - 特性
    - 切线与对应半径在切点处垂直
- 扇形
  - 定义
    - 由两个半径和连接这两个半径的弧所围成的区域
  - 面积计算
    - A = (θ/360) * πr²，θ为弧所对的中心角

## 性质
- 周长
  - 定义
    - 圆的外边界长度
  - 计算公式
    - C = 2πr
  - 性质
    - 与半径成正比
- 面积
  - 定义
    - 圆内部区域
  - 计算公式
    - A = πr²
  - 性质
    - 与半径的平方成正比
- 对称性
  - 特性
    - 圆是一个无限对称的图形
    - 任何通过圆心的直线都将圆分成两个相等的部分
  - 轴对称性
    - 任意直径都可作为对称轴

## 应用
- 几何学中的性质
  - 解决问题
    - 计算周长和面积
    - 角度和线段的关系
  - 推导定理
    - 利用圆的性质推导其他几何图形的性质
- 实际应用
  - 工程设计
  - 建筑学
  - 运动器材设计

图片