复变函数级数理论及应用
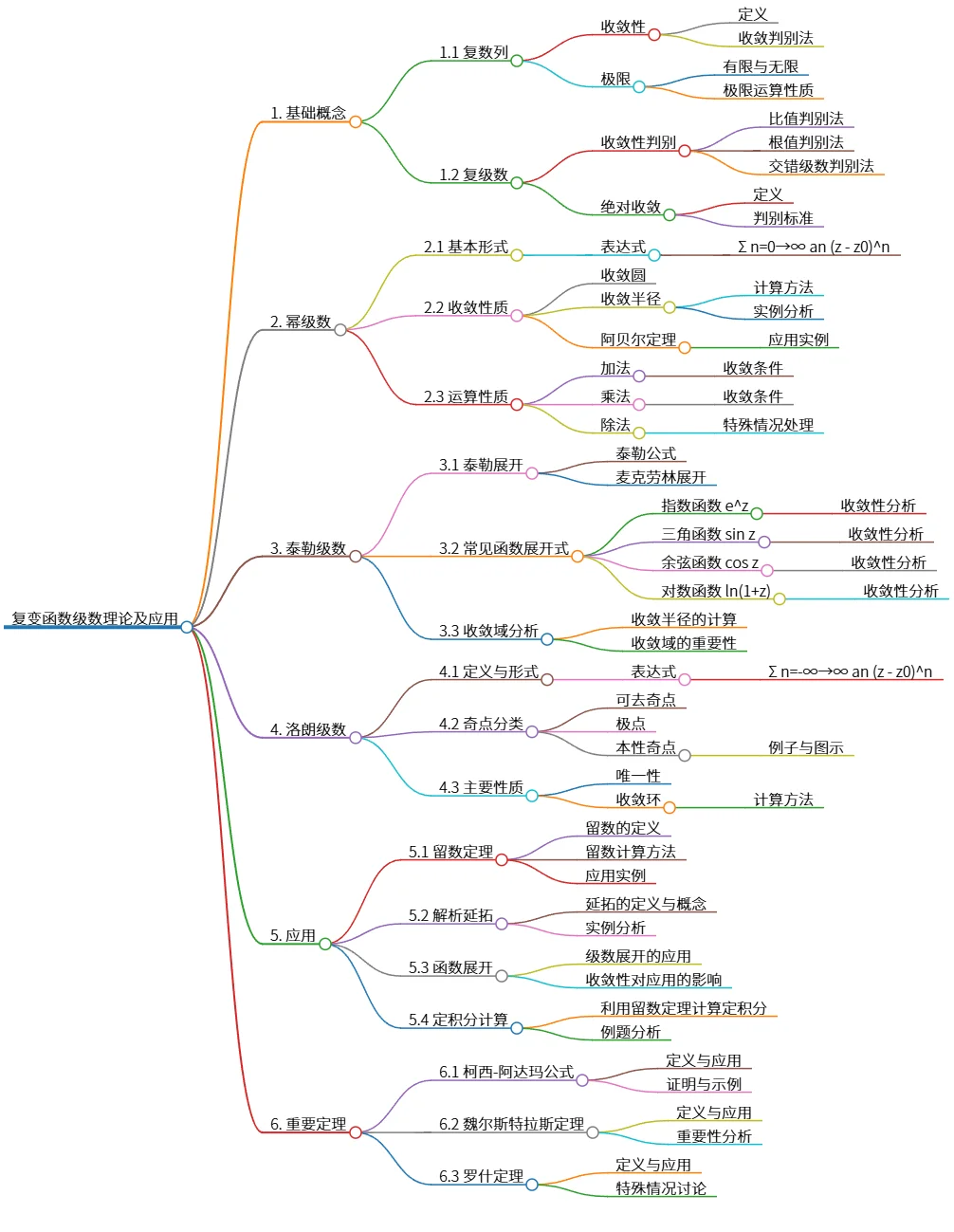
该思维导图概述了复变函数级数的知识体系,涵盖了复数列与复级数的基础概念,幂级数的收敛性质及运算,泰勒级数的展开与常见函数展开式,以及洛朗级数的定义、奇点分类和性质。此外,还涉及了复变函数级数在留数定理、解析延拓、函数展开和定积分计算等方面的应用,以及柯西-阿达玛公式、魏尔斯特拉斯定理和罗什定理等重要定理。 该思维导图系统地梳理了复变函数级数的核心内容和关键结论。
源码
# 复变函数级数理论及应用
## 1. 基础概念
### 1.1 复数列
- 收敛性
- 定义
- 收敛判别法
- 极限
- 有限与无限
- 极限运算性质
### 1.2 复级数
- 收敛性判别
- 比值判别法
- 根值判别法
- 交错级数判别法
- 绝对收敛
- 定义
- 判别标准
## 2. 幂级数
### 2.1 基本形式
- 表达式
- Σ n=0→∞ an (z - z0)^n
### 2.2 收敛性质
- 收敛圆
- 收敛半径
- 计算方法
- 实例分析
- 阿贝尔定理
- 应用实例
### 2.3 运算性质
- 加法
- 收敛条件
- 乘法
- 收敛条件
- 除法
- 特殊情况处理
## 3. 泰勒级数
### 3.1 泰勒展开
- 泰勒公式
- 麦克劳林展开
### 3.2 常见函数展开式
- 指数函数 e^z
- 收敛性分析
- 三角函数 sin z
- 收敛性分析
- 余弦函数 cos z
- 收敛性分析
- 对数函数 ln(1+z)
- 收敛性分析
### 3.3 收敛域分析
- 收敛半径的计算
- 收敛域的重要性
## 4. 洛朗级数
### 4.1 定义与形式
- 表达式
- Σ n=-∞→∞ an (z - z0)^n
### 4.2 奇点分类
- 可去奇点
- 极点
- 本性奇点
- 例子与图示
### 4.3 主要性质
- 唯一性
- 收敛环
- 计算方法
## 5. 应用
### 5.1 留数定理
- 留数的定义
- 留数计算方法
- 应用实例
### 5.2 解析延拓
- 延拓的定义与概念
- 实例分析
### 5.3 函数展开
- 级数展开的应用
- 收敛性对应用的影响
### 5.4 定积分计算
- 利用留数定理计算定积分
- 例题分析
## 6. 重要定理
### 6.1 柯西-阿达玛公式
- 定义与应用
- 证明与示例
### 6.2 魏尔斯特拉斯定理
- 定义与应用
- 重要性分析
### 6.3 罗什定理
- 定义与应用
- 特殊情况讨论
图片