抛物线建模与应用:初中二次函数实际探索与实践
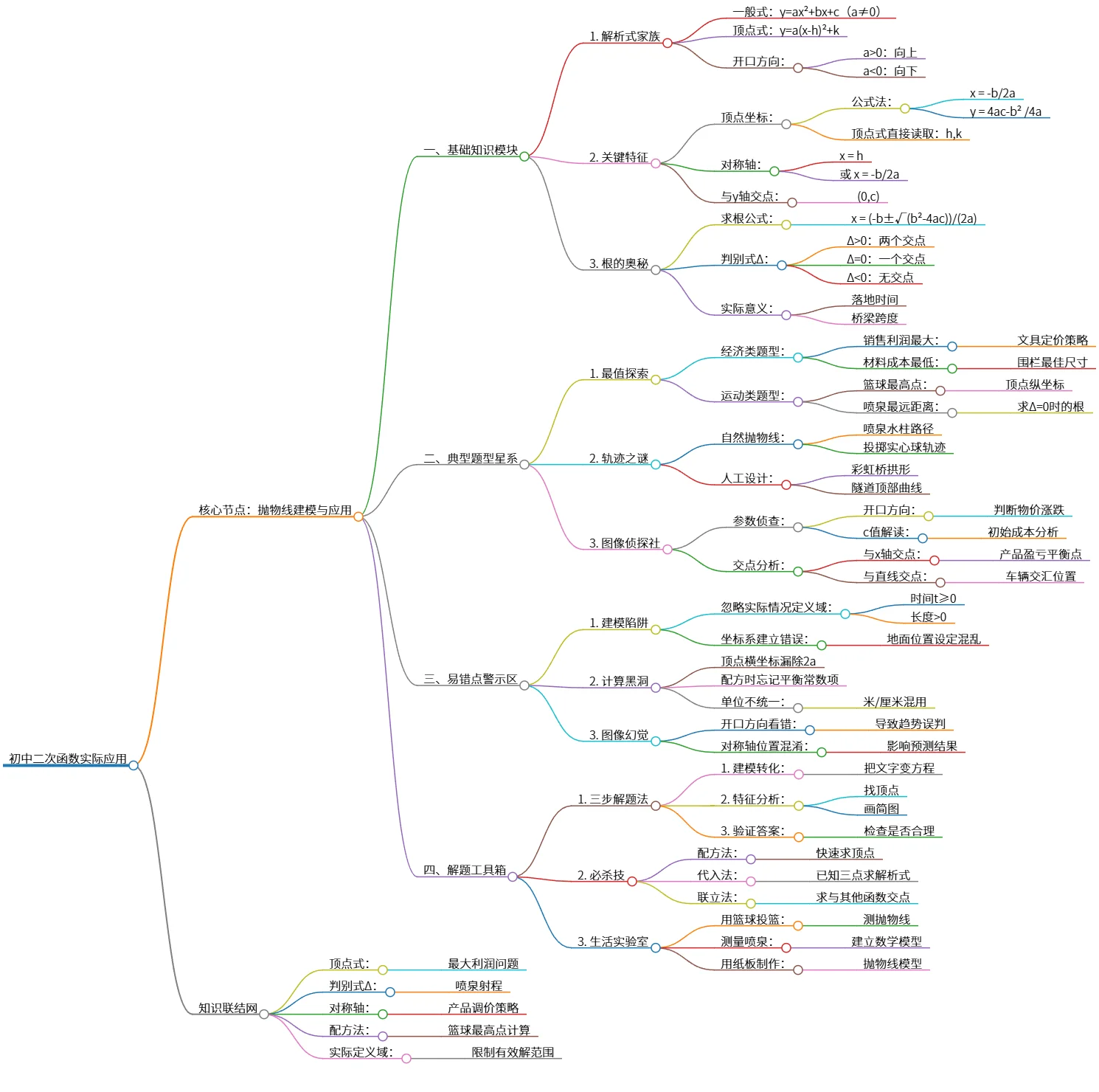
该思维导图围绕初中二次函数的抛物线建模与实际应用展开,涵盖基础知识、典型题型、易错点及解题工具。基础知识模块介绍解析式、特征和根的求解。典型题型分为最值探索、轨迹分析和图像分析,易错点警示区强调建模陷阱和计算错误。解题工具箱提供三步解题法和必杀技,鼓励实践与生活中的应用,展现数学在现实中的重要性和实用性。
源码
# 初中二次函数实际应用
## 核心节点:抛物线建模与应用
### 一、基础知识模块
#### 1. 解析式家族
- 一般式:y=ax²+bx+c(a≠0)
- 顶点式:y=a(x-h)²+k
- 开口方向:
- a>0:向上
- a<0:向下
#### 2. 关键特征
- 顶点坐标:
- 公式法:
- x = -b/2a
- y = 4ac-b² /4a
- 顶点式直接读取:h,k
- 对称轴:
- x = h
- 或 x = -b/2a
- 与y轴交点:
- (0,c)
#### 3. 根的奥秘
- 求根公式:
- x = (-b±√(b²-4ac))/(2a)
- 判别式Δ:
- Δ>0:两个交点
- Δ=0:一个交点
- Δ<0:无交点
- 实际意义:
- 落地时间
- 桥梁跨度
### 二、典型题型星系
#### 1. 最值探索
- 经济类题型:
- 销售利润最大:
- 文具定价策略
- 材料成本最低:
- 围栏最佳尺寸
- 运动类题型:
- 篮球最高点:
- 顶点纵坐标
- 喷泉最远距离:
- 求Δ=0时的根
#### 2. 轨迹之谜
- 自然抛物线:
- 喷泉水柱路径
- 投掷实心球轨迹
- 人工设计:
- 彩虹桥拱形
- 隧道顶部曲线
#### 3. 图像侦探社
- 参数侦查:
- 开口方向:
- 判断物价涨跌
- c值解读:
- 初始成本分析
- 交点分析:
- 与x轴交点:
- 产品盈亏平衡点
- 与直线交点:
- 车辆交汇位置
### 三、易错点警示区
#### 1. 建模陷阱
- 忽略实际情况定义域:
- 时间t≥0
- 长度>0
- 坐标系建立错误:
- 地面位置设定混乱
#### 2. 计算黑洞
- 顶点横坐标漏除2a
- 配方时忘记平衡常数项
- 单位不统一:
- 米/厘米混用
#### 3. 图像幻觉
- 开口方向看错:
- 导致趋势误判
- 对称轴位置混淆:
- 影响预测结果
### 四、解题工具箱
#### 1. 三步解题法
1. 建模转化:
- 把文字变方程
2. 特征分析:
- 找顶点
- 画简图
3. 验证答案:
- 检查是否合理
#### 2. 必杀技
- 配方法:
- 快速求顶点
- 代入法:
- 已知三点求解析式
- 联立法:
- 求与其他函数交点
#### 3. 生活实验室
- 用篮球投篮:
- 测抛物线
- 测量喷泉:
- 建立数学模型
- 用纸板制作:
- 抛物线模型
## 知识联结网
- 顶点式:
- 最大利润问题
- 判别式Δ:
- 喷泉射程
- 对称轴:
- 产品调价策略
- 配方法:
- 篮球最高点计算
- 实际定义域:
- 限制有效解范围
图片