自动控制原理:控制系统时域分析与性能指标探讨
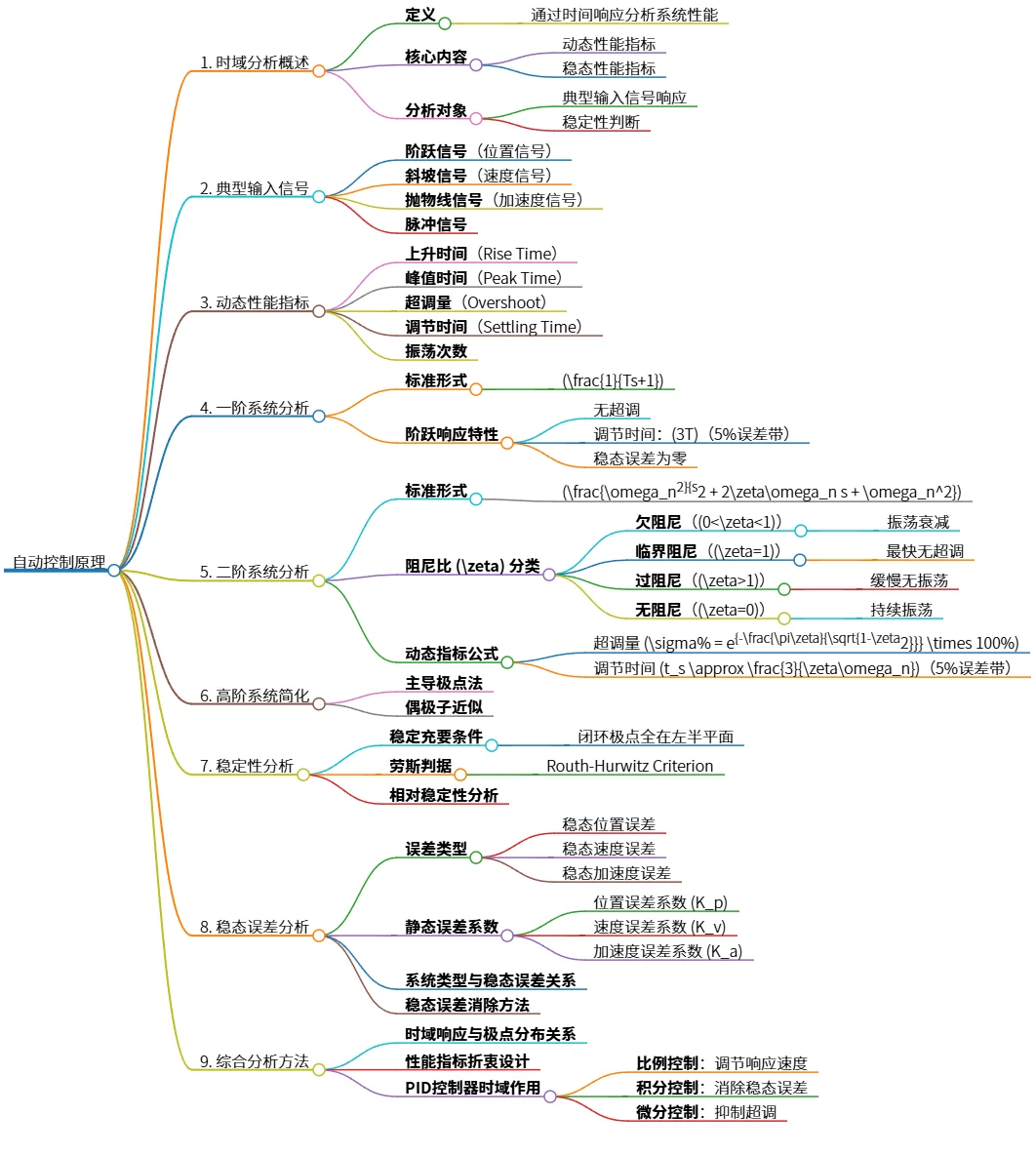
该思维导图概述了自动控制原理中的控制系统时域分析,包括时域分析的定义、典型输入信号、动态性能指标、以及一阶与二阶系统的分析。内容涉及稳定性分析、稳态误差分析和高阶系统的简化方法。同时,介绍了时域响应与极点分布的关系及PID控制器的作用,强调了各类控制方式对系统性能的影响。
源码
# 自动控制原理
## 1. 时域分析概述
- **定义**
- 通过时间响应分析系统性能
- **核心内容**
- 动态性能指标
- 稳态性能指标
- **分析对象**
- 典型输入信号响应
- 稳定性判断
## 2. 典型输入信号
- **阶跃信号**(位置信号)
- **斜坡信号**(速度信号)
- **抛物线信号**(加速度信号)
- **脉冲信号**
## 3. 动态性能指标
- **上升时间**(Rise Time)
- **峰值时间**(Peak Time)
- **超调量**(Overshoot)
- **调节时间**(Settling Time)
- **振荡次数**
## 4. 一阶系统分析
- **标准形式**
- \(\frac{1}{Ts+1}\)
- **阶跃响应特性**
- 无超调
- 调节时间:\(3T\)(5%误差带)
- 稳态误差为零
## 5. 二阶系统分析
- **标准形式**
- \(\frac{\omega_n^2}{s^2 + 2\zeta\omega_n s + \omega_n^2}\)
- **阻尼比 \(\zeta\) 分类**
- **欠阻尼**(\(0<\zeta<1\))
- 振荡衰减
- **临界阻尼**(\(\zeta=1\))
- 最快无超调
- **过阻尼**(\(\zeta>1\))
- 缓慢无振荡
- **无阻尼**(\(\zeta=0\))
- 持续振荡
- **动态指标公式**
- 超调量 \(\sigma\% = e^{-\frac{\pi\zeta}{\sqrt{1-\zeta^2}}} \times 100\%\)
- 调节时间 \(t_s \approx \frac{3}{\zeta\omega_n}\)(5%误差带)
## 6. 高阶系统简化
- **主导极点法**
- **偶极子近似**
## 7. 稳定性分析
- **稳定充要条件**
- 闭环极点全在左半平面
- **劳斯判据**
- Routh-Hurwitz Criterion
- **相对稳定性分析**
## 8. 稳态误差分析
- **误差类型**
- 稳态位置误差
- 稳态速度误差
- 稳态加速度误差
- **静态误差系数**
- 位置误差系数 \(K_p\)
- 速度误差系数 \(K_v\)
- 加速度误差系数 \(K_a\)
- **系统类型与稳态误差关系**
- **稳态误差消除方法**
## 9. 综合分析方法
- **时域响应与极点分布关系**
- **性能指标折衷设计**
- **PID控制器时域作用**
- **比例控制**:调节响应速度
- **积分控制**:消除稳态误差
- **微分控制**:抑制超调
图片