控制系统数学模型构建与分析的基础原理与方法
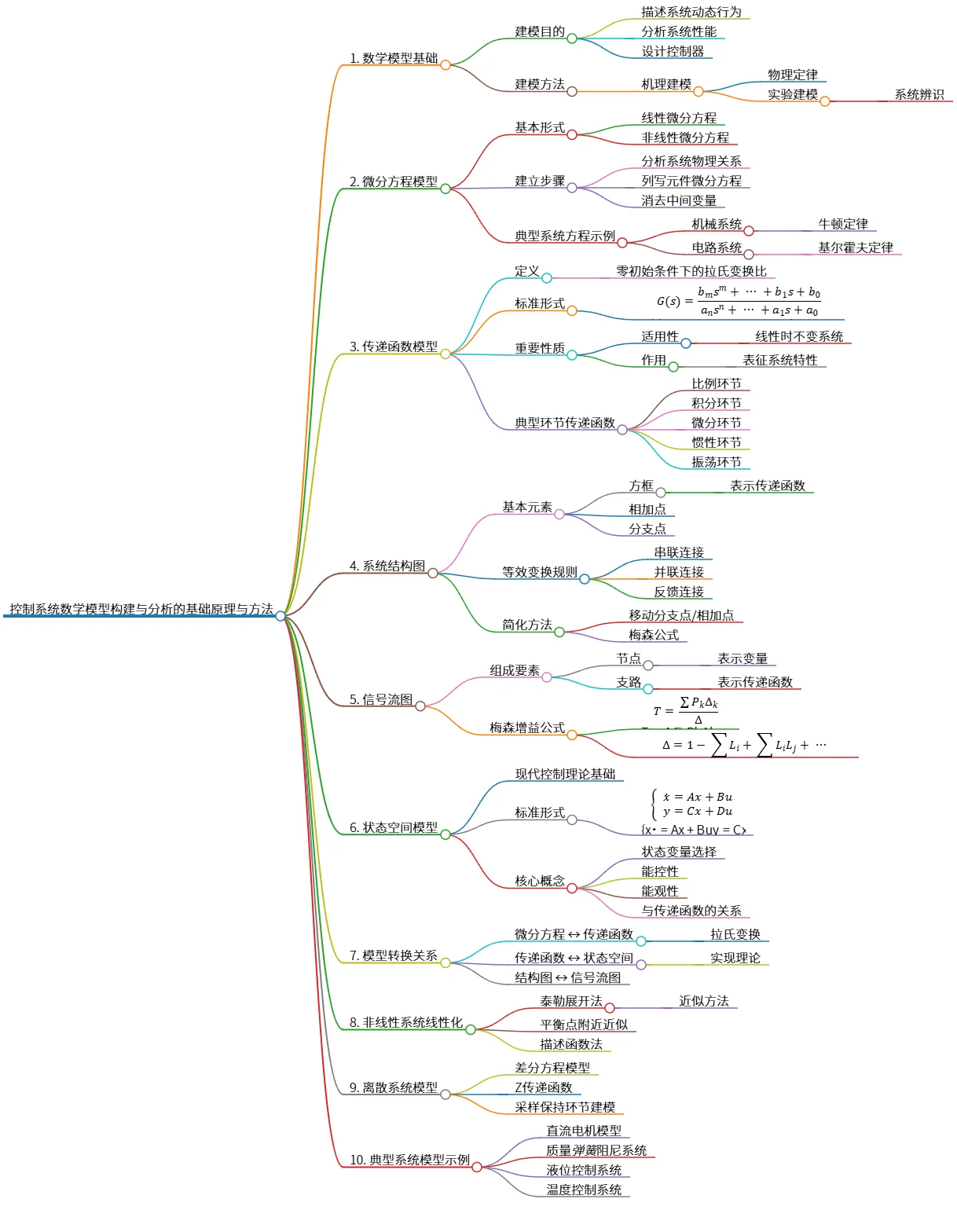
该思维导图概述了自动控制原理中的控制系统数学模型,包括数学模型基础、微分方程模型、传递函数模型、系统结构图、信号流图、状态空间模型等内容。它详细介绍了建模目的与方法、系统建模的核心形式、重要性质及典型模型示例,并探讨了模型转换关系、非线性系统线性化和离散系统模型。该内容为控制系统的分析与设计提供了理论依据。
源码
# 控制系统数学模型构建与分析的基础原理与方法
## 1. 数学模型基础
- 建模目的
- 描述系统动态行为
- 分析系统性能
- 设计控制器
- 建模方法
- 机理建模
- 物理定律
- 实验建模
- 系统辨识
## 2. 微分方程模型
- 基本形式
- 线性微分方程
- 非线性微分方程
- 建立步骤
- 分析系统物理关系
- 列写元件微分方程
- 消去中间变量
- 典型系统方程示例
- 机械系统
- 牛顿定律
- 电路系统
- 基尔霍夫定律
## 3. 传递函数模型
- 定义
- 零初始条件下的拉氏变换比
- 标准形式
- $$ G(s) = \frac{b_m s^m + \cdots + b_1 s + b_0}{a_n s^n + \cdots + a_1 s + a_0} $$
- 重要性质
- 适用性
- 线性时不变系统
- 作用
- 表征系统特性
- 典型环节传递函数
- 比例环节
- 积分环节
- 微分环节
- 惯性环节
- 振荡环节
## 4. 系统结构图
- 基本元素
- 方框
- 表示传递函数
- 相加点
- 分支点
- 等效变换规则
- 串联连接
- 并联连接
- 反馈连接
- 简化方法
- 移动分支点/相加点
- 梅森公式
## 5. 信号流图
- 组成要素
- 节点
- 表示变量
- 支路
- 表示传递函数
- 梅森增益公式
- $$ T = \frac{\sum P_k \Delta_k}{\Delta} $$
- $$ \Delta = 1 - \sum L_i + \sum L_i L_j + \cdots $$
## 6. 状态空间模型
- 现代控制理论基础
- 标准形式
- $$
\begin{cases}
\dot{x} = Ax + Bu \\
y = Cx + Du
\end{cases}
$$
- 核心概念
- 状态变量选择
- 能控性
- 能观性
- 与传递函数的关系
## 7. 模型转换关系
- 微分方程 ↔ 传递函数
- 拉氏变换
- 传递函数 ↔ 状态空间
- 实现理论
- 结构图 ↔ 信号流图
## 8. 非线性系统线性化
- 泰勒展开法
- 近似方法
- 平衡点附近近似
- 描述函数法
## 9. 离散系统模型
- 差分方程模型
- Z传递函数
- 采样保持环节建模
## 10. 典型系统模型示例
- 直流电机模型
- 质量_弹簧_阻尼系统
- 液位控制系统
- 温度控制系统
图片