极限计算方法及性质应用详解
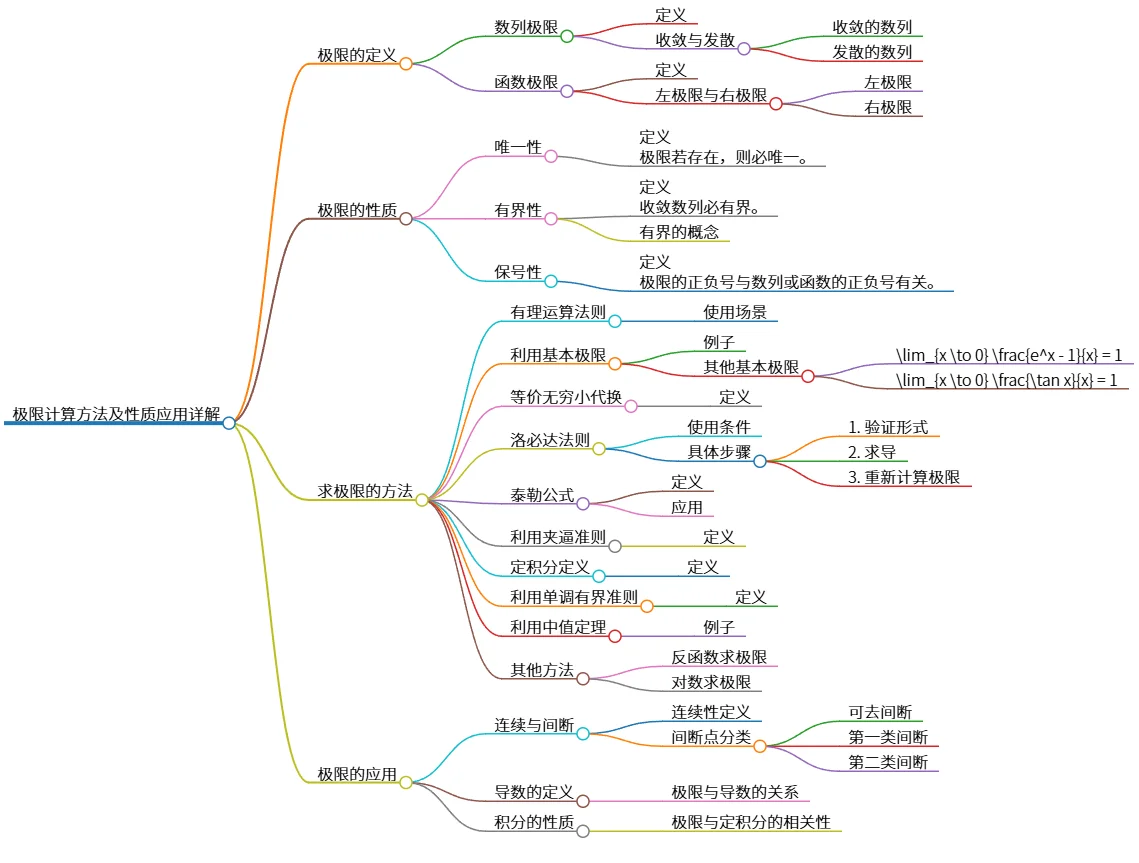
该思维导图概述了高等数学中极限的知识体系。涵盖了极限的定义(数列极限和函数极限),以及极限的性质(唯一性、有界性、保号性)。 求极限的方法则包括:有理运算法则、利用基本极限、等价无穷小代换、洛必达法则、泰勒公式、夹逼准则、定积分定义、单调有界准则和中值定理等多种技巧。最后,还提到了极限在判断函数连续性与间断性中的应用。 该图清晰地展现了极限概念及相关解题方法的逻辑结构。
源码
# 极限计算方法及性质应用详解
## 极限的定义
### 数列极限
#### 定义
描述数列趋近于某个常数的情况。
#### 收敛与发散
- 收敛的数列
- 发散的数列
### 函数极限
#### 定义
包括自变量趋近于有限值和无穷大的情况。
#### 左极限与右极限
- 左极限
- 右极限
## 极限的性质
### 唯一性
- 定义
极限若存在,则必唯一。
### 有界性
- 定义
收敛数列必有界。
- 有界的概念
### 保号性
- 定义
极限的正负号与数列或函数的正负号有关。
## 求极限的方法
### 有理运算法则
#### 使用场景
适用于有理函数的极限计算。
### 利用基本极限
#### 例子
如 \lim_{x \to 0} \frac{\sin x}{x} = 1 等。
#### 其他基本极限
- \lim_{x \to 0} \frac{e^x - 1}{x} = 1
- \lim_{x \to 0} \frac{\tan x}{x} = 1
### 等价无穷小代换
#### 定义
将一些无穷小量用等价的无穷小量替换。
### 洛必达法则
#### 使用条件
适用于 \frac{0}{0} 型或 \frac{\infty}{\infty} 型的极限计算。
#### 具体步骤
1. 验证形式
2. 求导
3. 重新计算极限
### 泰勒公式
#### 定义
将函数在某一点展开成泰勒级数。
#### 应用
用于求极限的近似值。
### 利用夹逼准则
#### 定义
通过找到两个函数,使得它们在某一点的极限相等,且夹在待求极限的函数之间。
### 定积分定义
#### 定义
对于某些数列极限,可以通过将其转化为定积分的形式来求解。
### 利用单调有界准则
#### 定义
适用于单调有界数列的极限计算。
### 利用中值定理
#### 例子
如拉格朗日中值定理等。
### 其他方法
- 反函数求极限
- 对数求极限
## 极限的应用
### 连续与间断
#### 连续性定义
判断函数在某一点的连续性。
#### 间断点分类
- 可去间断
- 第一类间断
- 第二类间断
### 导数的定义
- 极限与导数的关系
### 积分的性质
- 极限与定积分的相关性
图片