概率论的基本概念与重要定义解析与应用
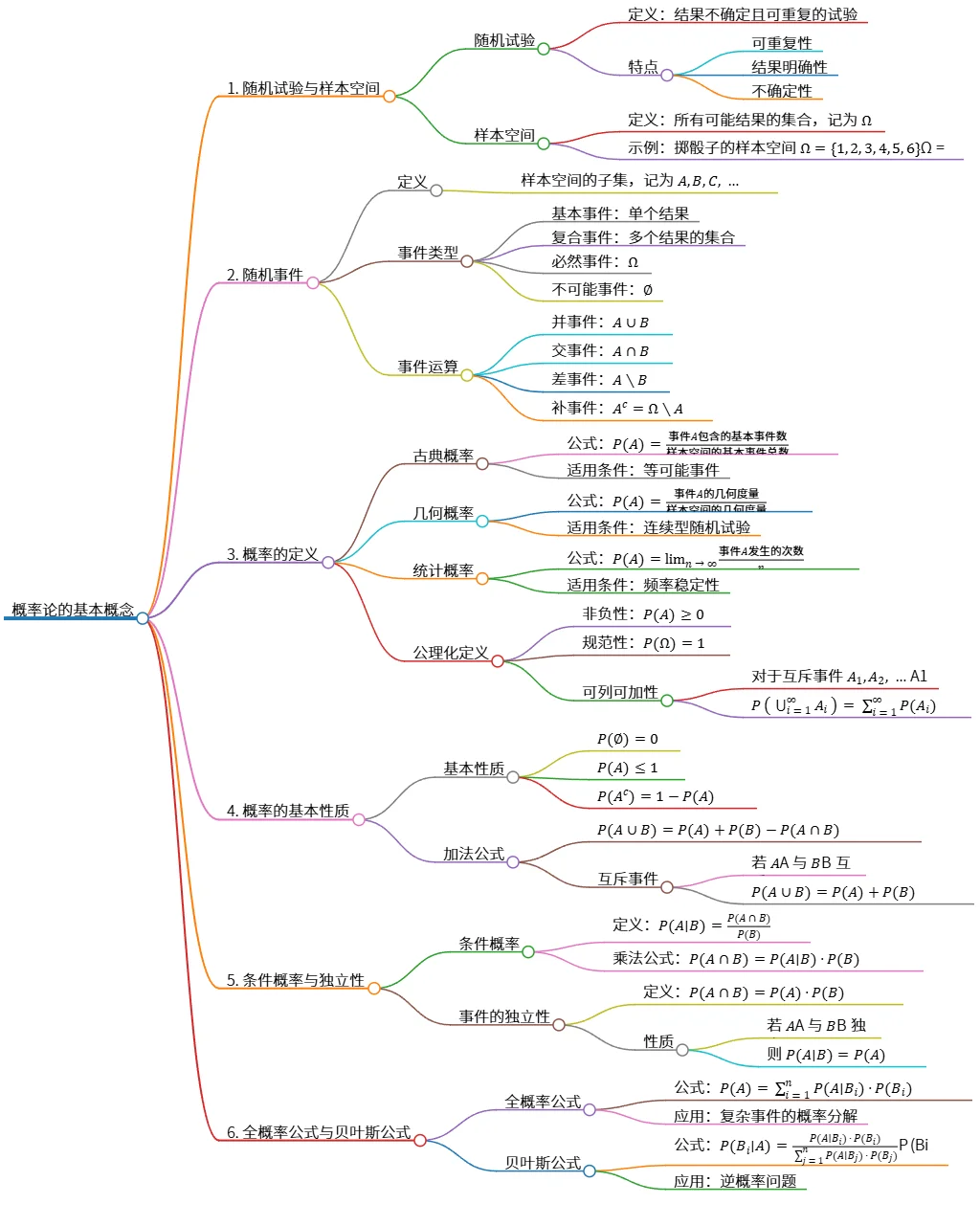
该思维导图概述了概率论的基本概念,包括随机试验、样本空间和随机事件的定义及分类,概率的不同定义(古典概率、几何概率、统计概率和公理化定义),以及基本性质和加法公式。此外,还讨论了条件概率和独立性,全概率公式及贝叶斯公式的应用。这些要点为理解和应用概率论奠定了基础。
源码
# 概率论的基本概念
## 1. 随机试验与样本空间
### 随机试验
- 定义:结果不确定且可重复的试验
- 特点
- 可重复性
- 结果明确性
- 不确定性
### 样本空间
- 定义:所有可能结果的集合,记为 $ \Omega $
- 示例:掷骰子的样本空间 $ \Omega = \{ 1, 2, 3, 4, 5, 6 \} $
## 2. 随机事件
### 定义
- 样本空间的子集,记为 $ A, B, C, \dots $
### 事件类型
- 基本事件:单个结果
- 复合事件:多个结果的集合
- 必然事件:$ \Omega $
- 不可能事件:$ \emptyset $
### 事件运算
- 并事件:$ A \cup B $
- 交事件:$ A \cap B $
- 差事件:$ A \setminus B $
- 补事件:$ A^c = \Omega \setminus A $
## 3. 概率的定义
### 古典概率
- 公式:$ P(A) = \frac{事件A包含的基本事件数}{样本空间的基本事件总数} $
- 适用条件:等可能事件
### 几何概率
- 公式:$ P(A) = \frac{事件A的几何度量}{样本空间的几何度量} $
- 适用条件:连续型随机试验
### 统计概率
- 公式:$ P(A) = \lim_{n \to \infty} \frac{事件A发生的次数}{n} $
- 适用条件:频率稳定性
### 公理化定义
- 非负性:$ P(A) \geq 0 $
- 规范性:$ P(\Omega) = 1 $
- 可列可加性
- 对于互斥事件 $ A_1, A_2, \dots $
- $ P\left( \bigcup_{i=1}^{\infty} A_i \right) = \sum_{i=1}^{\infty} P(A_i) $
## 4. 概率的基本性质
### 基本性质
- $ P(\emptyset) = 0 $
- $ P(A) \leq 1 $
- $ P(A^c) = 1 - P(A) $
### 加法公式
- $ P(A \cup B) = P(A) + P(B) - P(A \cap B) $
- 互斥事件
- 若 $ A $ 与 $ B $ 互斥
- $ P(A \cup B) = P(A) + P(B) $
## 5. 条件概率与独立性
### 条件概率
- 定义:$ P(A|B) = \frac{P(A \cap B)}{P(B)} $
- 乘法公式:$ P(A \cap B) = P(A|B) \cdot P(B) $
### 事件的独立性
- 定义:$ P(A \cap B) = P(A) \cdot P(B) $
- 性质
- 若 $ A $ 与 $ B $ 独立
- 则 $ P(A|B) = P(A) $
## 6. 全概率公式与贝叶斯公式
### 全概率公式
- 公式:$ P(A) = \sum_{i=1}^{n} P(A|B_i) \cdot P(B_i) $
- 应用:复杂事件的概率分解
### 贝叶斯公式
- 公式:$ P(B_i|A) = \frac{P(A|B_i) \cdot P(B_i)}{\sum_{j=1}^{n} P(A|B_j) \cdot P(B_j)} $
- 应用:逆概率问题
图片