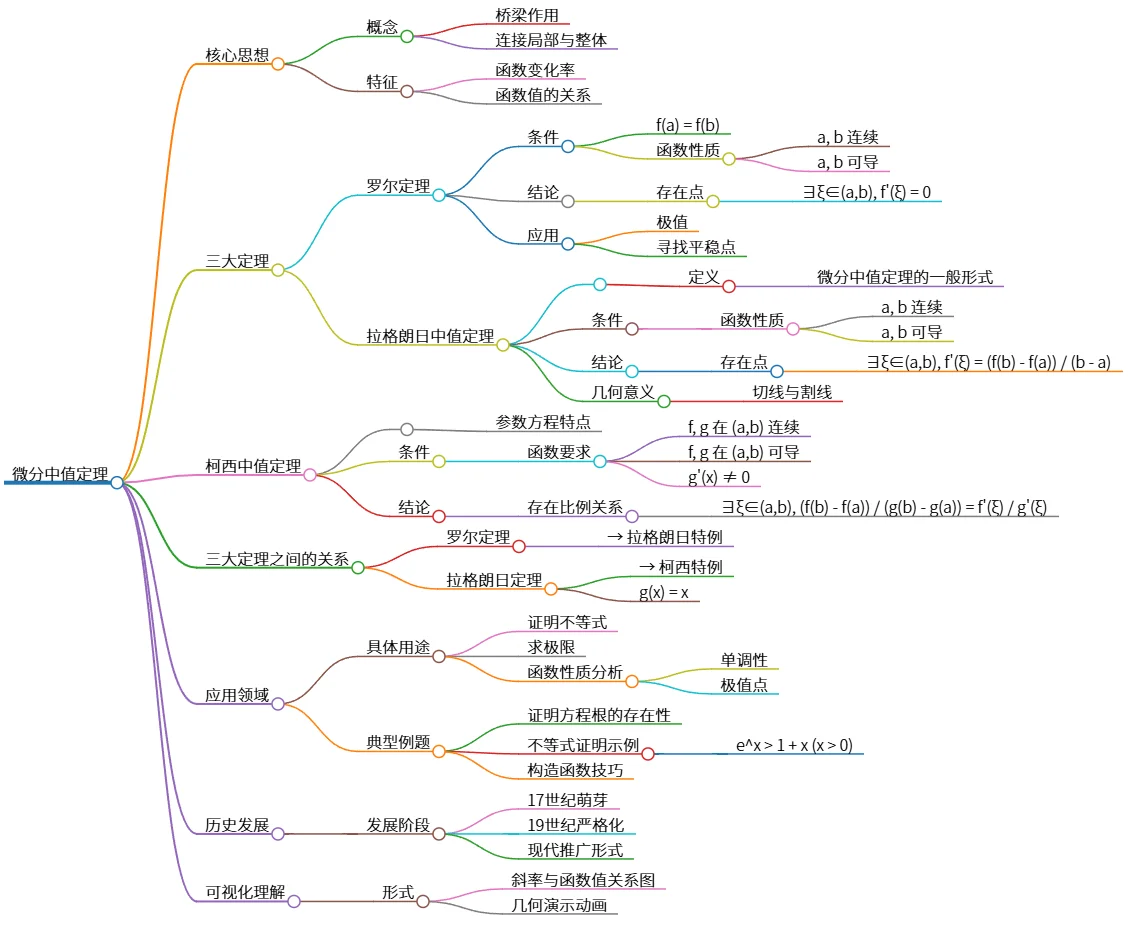
微分中值定理的核心思想、定理及应用分析

# 微分中值定理
## 核心思想
- 概念
  - 桥梁作用
  - 连接局部与整体
- 特征
  - 函数变化率
  - 函数值的关系
## 三大定理
### 罗尔定理
#### 条件
- f(a) = f(b)
- 函数性质
  - a, b 连续
  - a, b 可导
#### 结论
- 存在点
  - ∃ξ∈(a,b), f'(ξ) = 0
#### 应用
- 极值
- 寻找平稳点
### 拉格朗日中值定理
- 定义
  - 微分中值定理的一般形式
#### 条件
- 函数性质
  - a, b 连续
  - a, b 可导
#### 结论
- 存在点
  - ∃ξ∈(a,b), f'(ξ) = (f(b) - f(a)) / (b - a)
#### 几何意义
- 切线与割线
## 柯西中值定理
- 参数方程特点
#### 条件
- 函数要求
  - f, g 在 (a,b) 连续
  - f, g 在 (a,b) 可导
  - g'(x) ≠ 0
#### 结论
- 存在比例关系
  - ∃ξ∈(a,b), (f(b) - f(a)) / (g(b) - g(a)) = f'(ξ) / g'(ξ)
## 三大定理之间的关系
- 罗尔定理
  - → 拉格朗日特例
- 拉格朗日定理
  - → 柯西特例
  - g(x) = x
## 应用领域
- 具体用途
  - 证明不等式
  - 求极限
  - 函数性质分析
    - 单调性
    - 极值点
- 典型例题
  - 证明方程根的存在性
  - 不等式证明示例
    - e^x > 1 + x (x > 0)
  - 构造函数技巧
## 历史发展
- 发展阶段
  - 17世纪萌芽
  - 19世纪严格化
  - 现代推广形式
## 可视化理解
- 形式
  - 斜率与函数值关系图
  - 几何演示动画