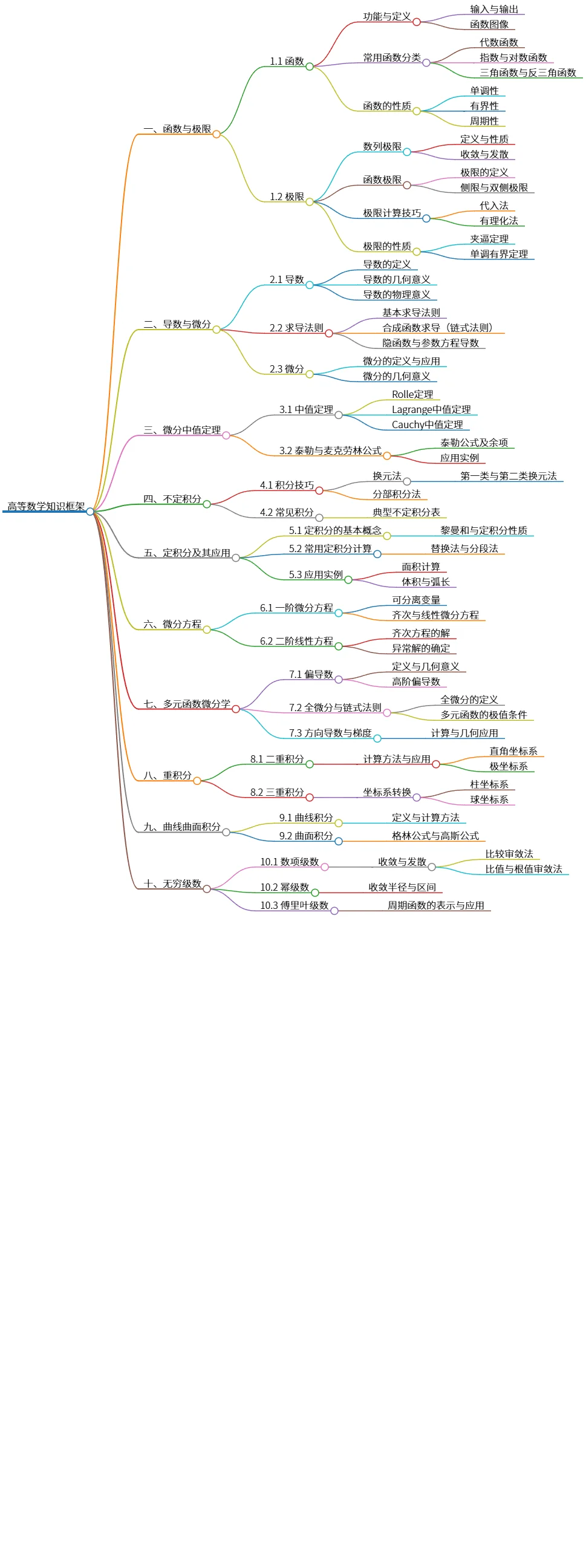
高等数学知识框架：函数、导数、积分与无穷级数概述

# 高等数学知识框架
## 一、函数与极限
### 1.1 函数
- 功能与定义
  - 输入与输出
  - 函数图像
- 常用函数分类
  - 代数函数
  - 指数与对数函数
  - 三角函数与反三角函数
- 函数的性质
  - 单调性
  - 有界性
  - 周期性
### 1.2 极限
- 数列极限
  - 定义与性质
  - 收敛与发散
- 函数极限
  - 极限的定义
  - 侧限与双侧极限
- 极限计算技巧
  - 代入法
  - 有理化法
- 极限的性质
  - 夹逼定理
  - 单调有界定理
## 二、导数与微分
### 2.1 导数
- 导数的定义
- 导数的几何意义
- 导数的物理意义
### 2.2 求导法则
- 基本求导法则
- 合成函数求导（链式法则）
- 隐函数与参数方程导数
### 2.3 微分
- 微分的定义与应用
- 微分的几何意义
## 三、微分中值定理
### 3.1 中值定理
- Rolle定理
- Lagrange中值定理
- Cauchy中值定理
### 3.2 泰勒与麦克劳林公式
- 泰勒公式及余项
- 应用实例
## 四、不定积分
### 4.1 积分技巧
- 换元法
  - 第一类与第二类换元法
- 分部积分法
### 4.2 常见积分
- 典型不定积分表
## 五、定积分及其应用
### 5.1 定积分的基本概念
- 黎曼和与定积分性质
### 5.2 常用定积分计算
- 替换法与分段法
### 5.3 应用实例
- 面积计算
- 体积与弧长
## 六、微分方程
### 6.1 一阶微分方程
- 可分离变量
- 齐次与线性微分方程
### 6.2 二阶线性方程
- 齐次方程的解
- 异常解的确定
## 七、多元函数微分学
### 7.1 偏导数
- 定义与几何意义
- 高阶偏导数
### 7.2 全微分与链式法则
- 全微分的定义
- 多元函数的极值条件
### 7.3 方向导数与梯度
- 计算与几何应用
## 八、重积分
### 8.1 二重积分
- 计算方法与应用
  - 直角坐标系
  - 极坐标系
### 8.2 三重积分
- 坐标系转换
  - 柱坐标系
  - 球坐标系
## 九、曲线曲面积分
### 9.1 曲线积分
- 定义与计算方法
### 9.2 曲面积分
- 格林公式与高斯公式
## 十、无穷级数
### 10.1 数项级数
- 收敛与发散
  - 比较审敛法
  - 比值与根值审敛法
### 10.2 幂级数
- 收敛半径与区间
### 10.3 傅里叶级数
- 周期函数的表示与应用