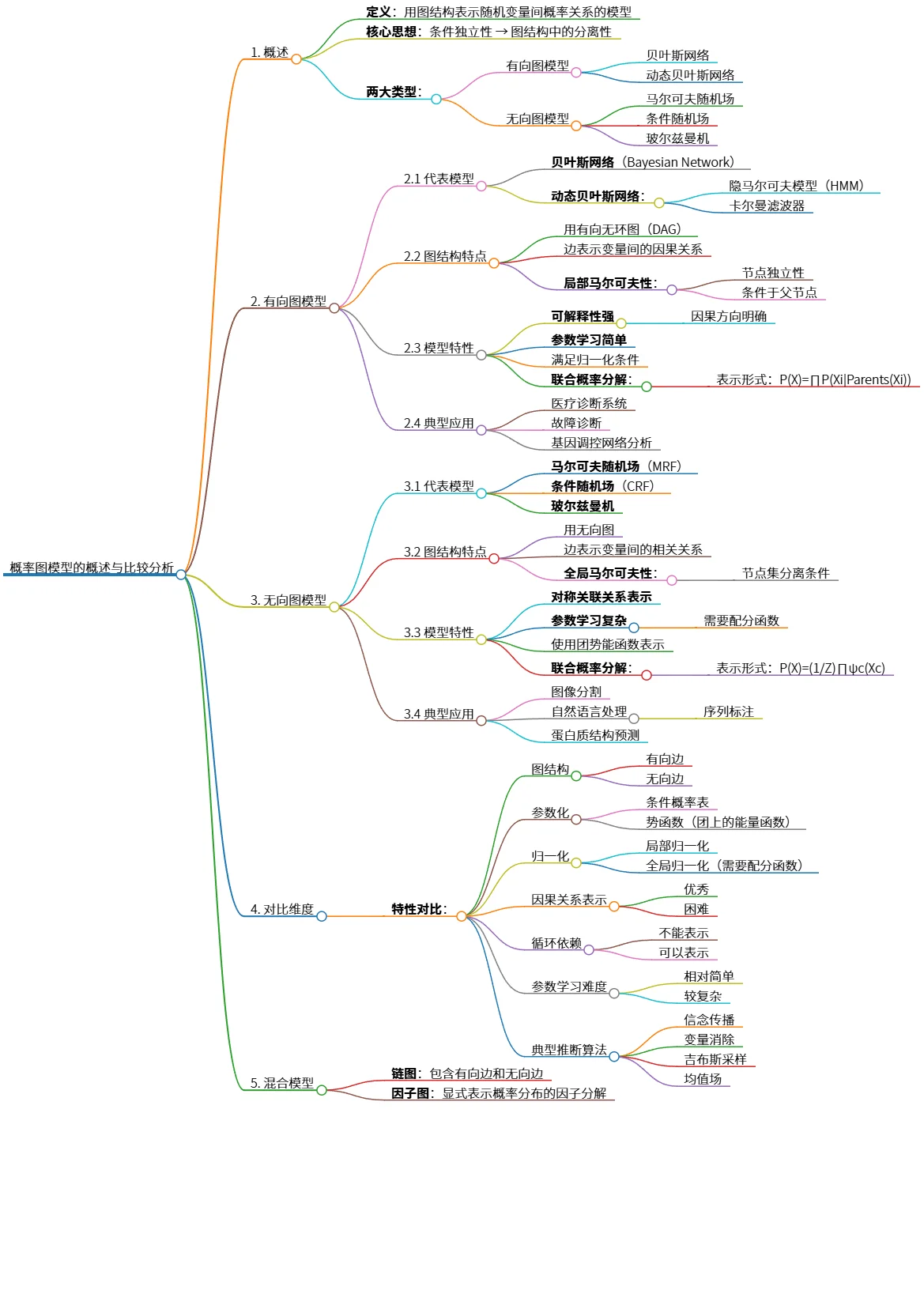
概率图模型的概述与比较分析：有向与无向模型

# 概率图模型的概述与比较分析
## 1. 概述
- **定义**：用图结构表示随机变量间概率关系的模型
- **核心思想**：条件独立性 → 图结构中的分离性
- **两大类型**：
  - 有向图模型
    - 贝叶斯网络
    - 动态贝叶斯网络
  - 无向图模型
    - 马尔可夫随机场
    - 条件随机场
    - 玻尔兹曼机
  
## 2. 有向图模型
### 2.1 代表模型
- **贝叶斯网络**（Bayesian Network）
- **动态贝叶斯网络**：
  - 隐马尔可夫模型（HMM）
  - 卡尔曼滤波器
  
### 2.2 图结构特点
- 用有向无环图（DAG）
- 边表示变量间的因果关系
- **局部马尔可夫性**：
  - 节点独立性
  - 条件于父节点
  
### 2.3 模型特性
- **可解释性强**
  - 因果方向明确
- **参数学习简单**
- 满足归一化条件
- **联合概率分解**：
  - 表示形式：P(X)=∏P(Xi|Parents(Xi))
  
### 2.4 典型应用
- 医疗诊断系统
- 故障诊断
- 基因调控网络分析
  
## 3. 无向图模型
### 3.1 代表模型
- **马尔可夫随机场**（MRF）
- **条件随机场**（CRF）
- **玻尔兹曼机**
  
### 3.2 图结构特点
- 用无向图
- 边表示变量间的相关关系
- **全局马尔可夫性**：
  - 节点集分离条件
  
### 3.3 模型特性
- **对称关联关系表示**
- **参数学习复杂**
  - 需要配分函数
- 使用团势能函数表示
- **联合概率分解**：
  - 表示形式：P(X)=(1/Z)∏ψc(Xc)
  
### 3.4 典型应用
- 图像分割
- 自然语言处理
  - 序列标注
- 蛋白质结构预测
  
## 4. 对比维度
- **特性对比**：
  - 图结构
    - 有向边
    - 无向边
  - 参数化
    - 条件概率表
    - 势函数（团上的能量函数）
  - 归一化
    - 局部归一化
    - 全局归一化（需要配分函数）
  - 因果关系表示
    - 优秀
    - 困难
  - 循环依赖
    - 不能表示
    - 可以表示
  - 参数学习难度
    - 相对简单
    - 较复杂
  - 典型推断算法
    - 信念传播
    - 变量消除
    - 吉布斯采样
    - 均值场
  
## 5. 混合模型
- **链图**：包含有向边和无向边
- **因子图**：显式表示概率分布的因子分解