导数及其应用：概念、计算、性质与实际问题解析

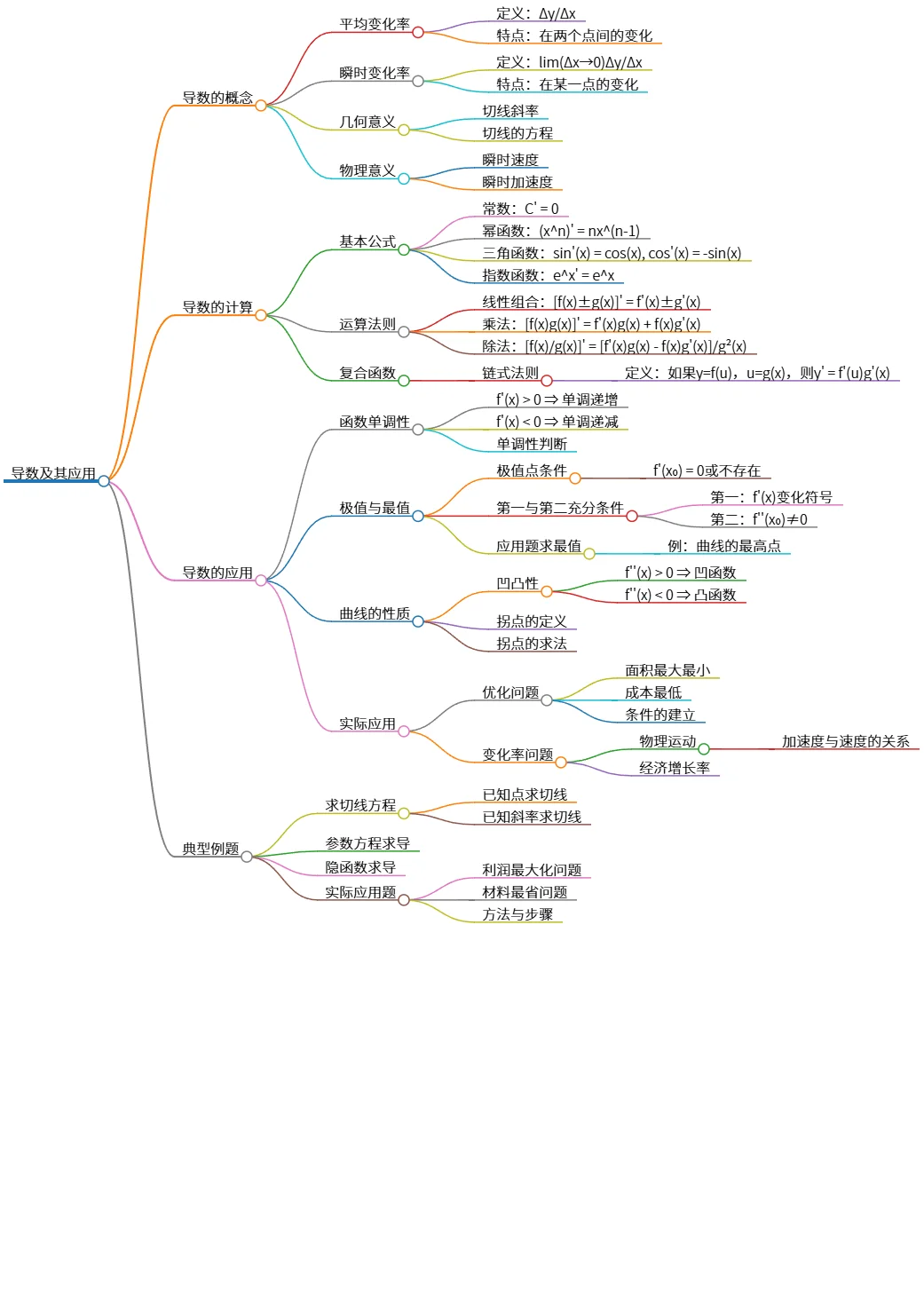
该思维导图概述了导数的基本概念、计算方法及其应用。介绍了平均变化率与瞬时变化率的定义和几何、物理意义；列出了导数的基本计算公式和运算法则，包括复合函数的链式法则。在应用部分，探讨了函数的单调性、极值与最值、曲线性质及实际应用，如优化问题和变化率问题。最后，通过典型例题展示求切线方程、参数方程和隐函数求导的具体计算。

源码

# 导数及其应用
- 导数的概念
  - 平均变化率
    - 定义：Δy/Δx
    - 特点：在两个点间的变化
  - 瞬时变化率
    - 定义：lim(Δx→0)Δy/Δx
    - 特点：在某一点的变化
  - 几何意义
    - 切线斜率
    - 切线的方程
  - 物理意义
    - 瞬时速度
    - 瞬时加速度
- 导数的计算
  - 基本公式
    - 常数：C' = 0
    - 幂函数：(x^n)' = nx^(n-1)
    - 三角函数：sin'(x) = cos(x), cos'(x) = -sin(x)
    - 指数函数：e^x' = e^x
  - 运算法则
    - 线性组合：[f(x)±g(x)]' = f'(x)±g'(x)
    - 乘法：[f(x)g(x)]' = f'(x)g(x) + f(x)g'(x)
    - 除法：[f(x)/g(x)]' = [f'(x)g(x) - f(x)g'(x)]/g²(x)
  - 复合函数
    - 链式法则
      - 定义：如果y=f(u)，u=g(x)，则y' = f'(u)g'(x)
- 导数的应用
  - 函数单调性
    - f'(x) > 0 ⇒ 单调递增
    - f'(x) < 0 ⇒ 单调递减
    - 单调性判断
  - 极值与最值
    - 极值点条件
      - f'(x₀) = 0或不存在
    - 第一与第二充分条件
      - 第一：f'(x)变化符号
      - 第二：f''(x₀)≠0
    - 应用题求最值
      - 例：曲线的最高点
  - 曲线的性质
    - 凹凸性
      - f''(x) > 0 ⇒ 凹函数
      - f''(x) < 0 ⇒ 凸函数
    - 拐点的定义
    - 拐点的求法
  - 实际应用
    - 优化问题
      - 面积最大最小
      - 成本最低
      - 条件的建立
    - 变化率问题
      - 物理运动
        - 加速度与速度的关系
      - 经济增长率
- 典型例题
  - 求切线方程
    - 已知点求切线
    - 已知斜率求切线
  - 参数方程求导
  - 隐函数求导
  - 实际应用题
    - 利润最大化问题
    - 材料最省问题
    - 方法与步骤

图片