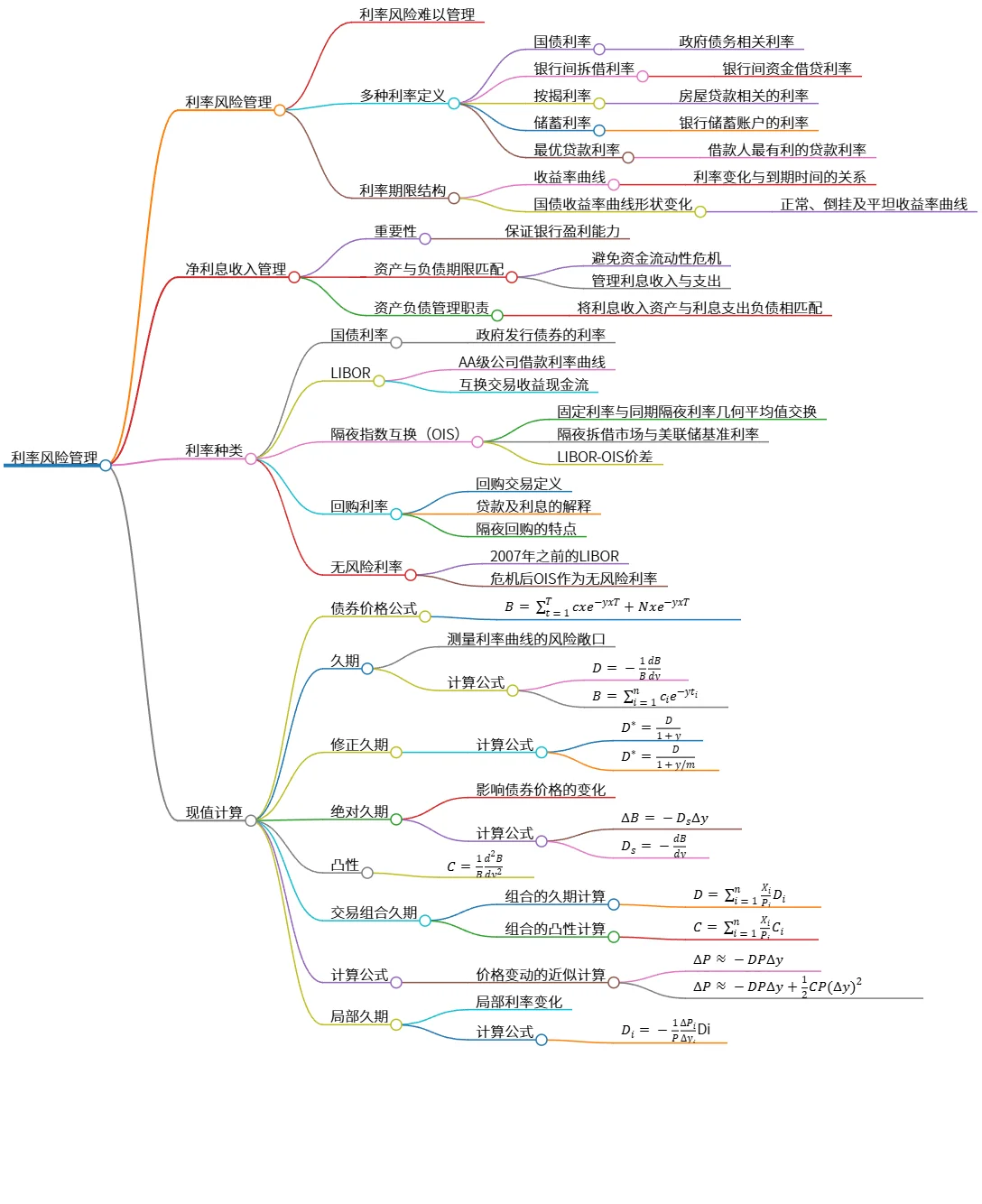
利率风险管理与净利息收入管理的综合探讨

# 利率风险管理
## 利率风险管理
- 利率风险难以管理
- 多种利率定义
  - 国债利率
    - 政府债务相关利率
  - 银行间拆借利率
    - 银行间资金借贷利率
  - 按揭利率
    - 房屋贷款相关的利率
  - 储蓄利率
    - 银行储蓄账户的利率
  - 最优贷款利率
    - 借款人最有利的贷款利率
- 利率期限结构
  - 收益率曲线
    - 利率变化与到期时间的关系
  - 国债收益率曲线形状变化
    - 正常、倒挂及平坦收益率曲线
## 净利息收入管理
- 重要性
  - 保证银行盈利能力
- 资产与负债期限匹配
  - 避免资金流动性危机
  - 管理利息收入与支出
- 资产负债管理职责
  - 将利息收入资产与利息支出负债相匹配
## 利率种类
- 国债利率
  - 政府发行债券的利率
- LIBOR
  - AA级公司借款利率曲线
  - 互换交易收益现金流
- 隔夜指数互换（OIS）
  - 固定利率与同期隔夜利率几何平均值交换
  - 隔夜拆借市场与美联储基准利率
  - LIBOR-OIS价差
- 回购利率
  - 回购交易定义
  - 贷款及利息的解释
  - 隔夜回购的特点
- 无风险利率
  - 2007年之前的LIBOR
  - 危机后OIS作为无风险利率
## 现值计算
- 债券价格公式
  - $B = \sum_{t=1}^{T} cxe^{-yxT} + Nxe^{-yxT}$
- 久期
  - 测量利率曲线的风险敞口
  - 计算公式
    - $D = -\frac{1}{B} \frac{dB}{dy}$
    - $B = \sum_{i=1}^{n} c_i e^{-y t_i}$
- 修正久期
  - 计算公式
    - $D^{*}=\frac{D}{1+y}$
    - $D^{*}=\frac{D}{1+y/m}$
- 绝对久期
  - 影响债券价格的变化
  - 计算公式
    - $\Delta B=-D_{s}\Delta y$
    - $D_{s}=-\frac{dB}{dy}$
- 凸性
  - $C=\frac{1}{B}\frac{d^{2}B}{dy^{2}}$
- 交易组合久期
  - 组合的久期计算
    - $D = \sum_{i=1}^{n} \frac{X_i}{P_i} D_i$
  - 组合的凸性计算
    - $C = \sum_{i=1}^{n} \frac{X_i}{P_i} C_i$
- 计算公式
  - 价格变动的近似计算
    - $\Delta P \approx -DP\Delta y$
    - $\Delta P \approx -DP\Delta y + \frac{1}{2}CP(\Delta y)^2$
- 局部久期
  - 局部利率变化
  - 计算公式
    - $D_i=-\frac{1}{P}\frac{\Delta P_i}{\Delta y_i}$