一次方程组与解法及应用题解析
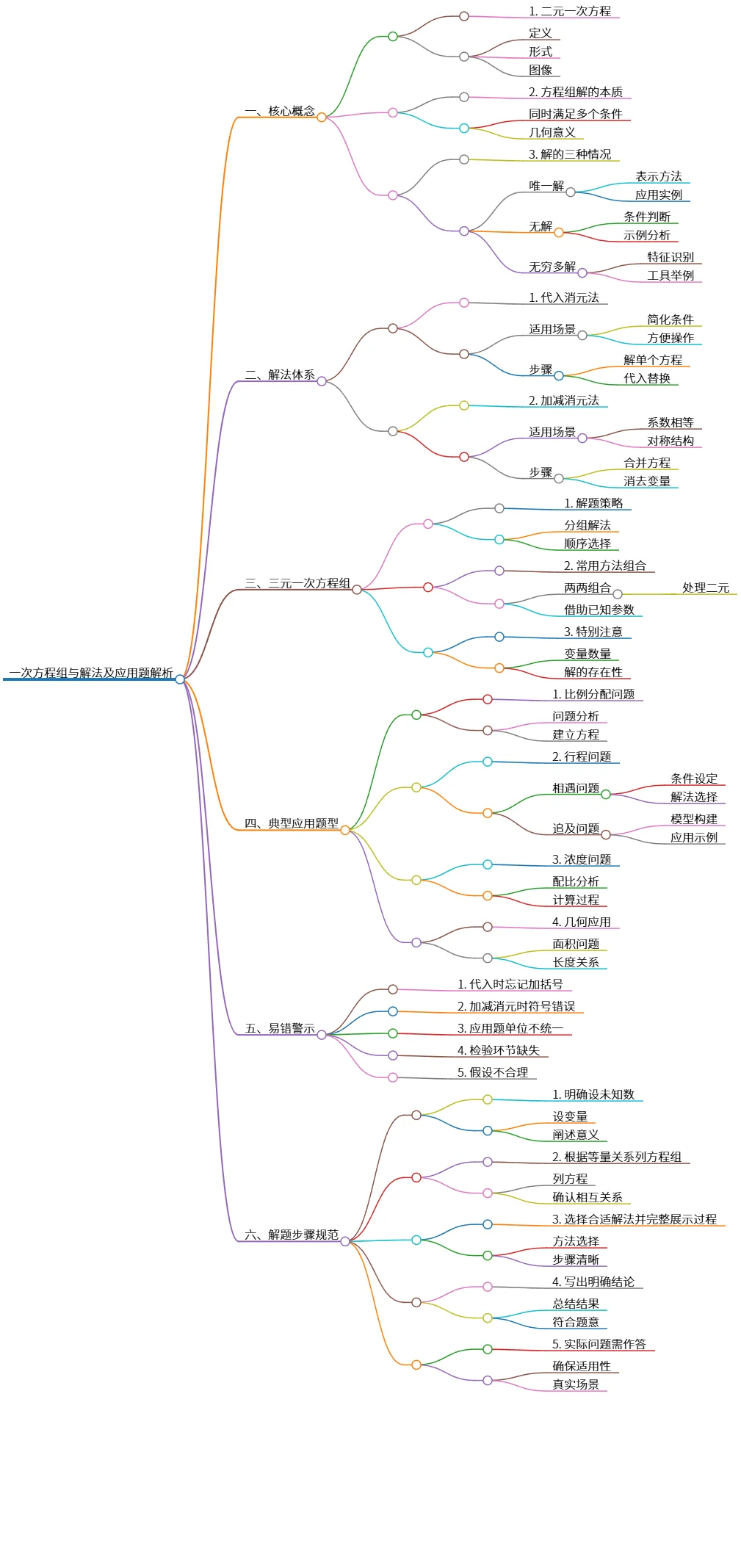
该思维导图概述了一次方程组的核心概念、解法体系及应用。重点介绍了二元一次方程的解的三种情况及两种解法(代入消元法和加减消元法)。此外,还讨论了三元一次方程组的解题策略、典型应用题型如比例分配和行程问题,以及常见的易错警示。最后,强调了解题步骤的规范,确保问题的准确解答。
源码
# 一次方程组与解法及应用题解析
- 一、核心概念
- 1. 二元一次方程
- 定义
- 形式
- 图像
- 2. 方程组解的本质
- 同时满足多个条件
- 几何意义
- 3. 解的三种情况
- 唯一解
- 表示方法
- 应用实例
- 无解
- 条件判断
- 示例分析
- 无穷多解
- 特征识别
- 工具举例
- 二、解法体系
- 1. 代入消元法
- 适用场景
- 简化条件
- 方便操作
- 步骤
- 解单个方程
- 代入替换
- 2. 加减消元法
- 适用场景
- 系数相等
- 对称结构
- 步骤
- 合并方程
- 消去变量
- 三、三元一次方程组
- 1. 解题策略
- 分组解法
- 顺序选择
- 2. 常用方法组合
- 两两组合
- 处理二元
- 借助已知参数
- 3. 特别注意
- 变量数量
- 解的存在性
- 四、典型应用题型
- 1. 比例分配问题
- 问题分析
- 建立方程
- 2. 行程问题
- 相遇问题
- 条件设定
- 解法选择
- 追及问题
- 模型构建
- 应用示例
- 3. 浓度问题
- 配比分析
- 计算过程
- 4. 几何应用
- 面积问题
- 长度关系
- 五、易错警示
- 1. 代入时忘记加括号
- 2. 加减消元时符号错误
- 3. 应用题单位不统一
- 4. 检验环节缺失
- 5. 假设不合理
- 六、解题步骤规范
- 1. 明确设未知数
- 设变量
- 阐述意义
- 2. 根据等量关系列方程组
- 列方程
- 确认相互关系
- 3. 选择合适解法并完整展示过程
- 方法选择
- 步骤清晰
- 4. 写出明确结论
- 总结结果
- 符合题意
- 5. 实际问题需作答
- 确保适用性
- 真实场景
图片