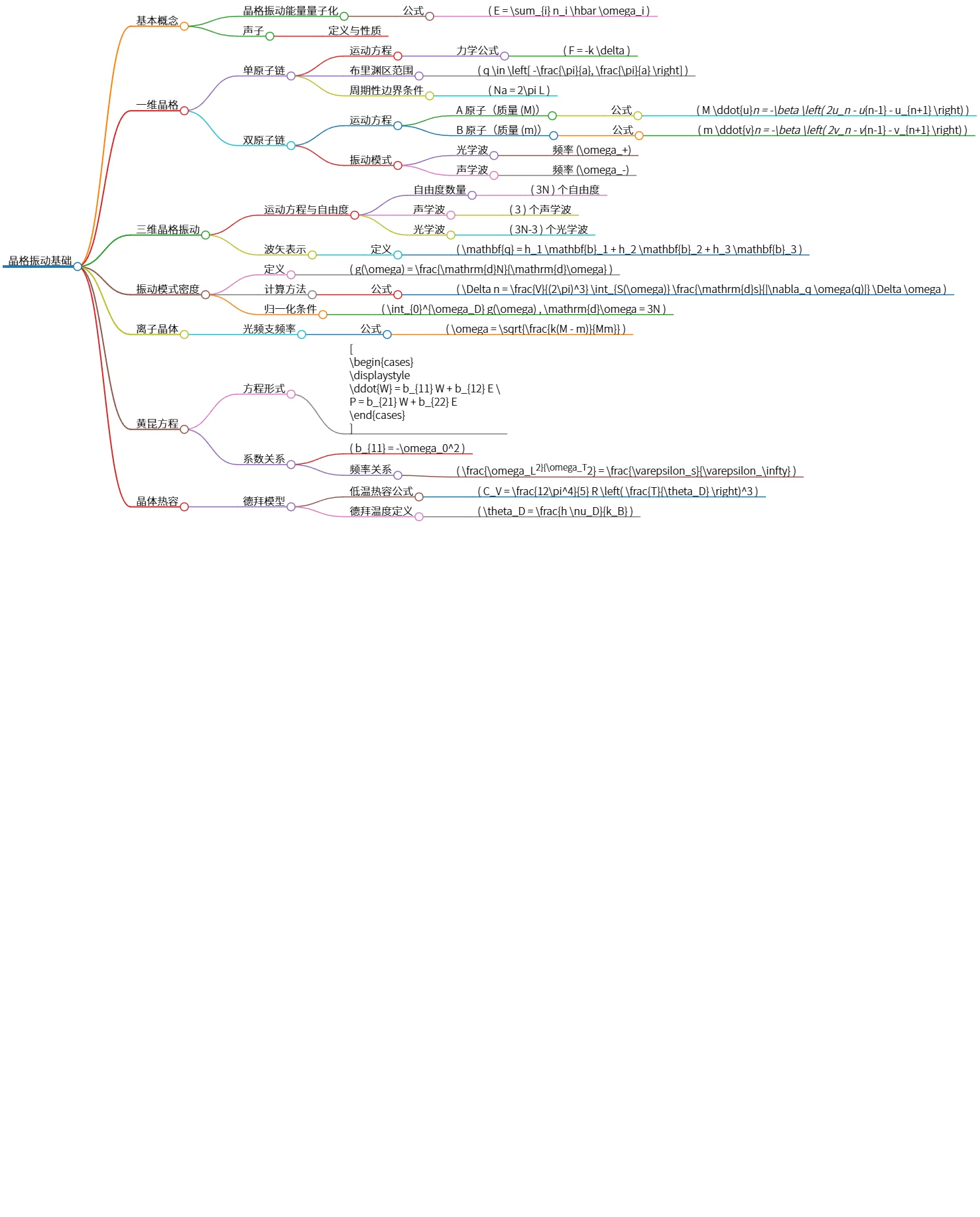
晶格振动基础：声子、频率、热容与模型解析

# 晶格振动基础
- 基本概念
  - 晶格振动能量量子化
    - 公式
      - \( E = \sum_{i} n_i \hbar \omega_i \)
  - 声子
    - 定义与性质
- 一维晶格
  - 单原子链
    - 运动方程
      - 力学公式
        - \( F = -k \delta \)
    - 布里渊区范围
      - \( q \in \left[ -\frac{\pi}{a}, \frac{\pi}{a} \right] \)
    - 周期性边界条件
      - \( Na = 2\pi L \)
  - 双原子链
    - 运动方程
      - A 原子（质量 \(M\)）
        - 公式
          - \( M \ddot{u}_n = -\beta \left( 2u_n - u_{n-1} - u_{n+1} \right) \)
      - B 原子（质量 \(m\)）
        - 公式
          - \( m \ddot{v}_n = -\beta \left( 2v_n - v_{n-1} - v_{n+1} \right) \)
    - 振动模式
      - 光学波
        - 频率 \(\omega_+\)
      - 声学波
        - 频率 \(\omega_-\)
- 三维晶格振动
  - 运动方程与自由度
    - 自由度数量
      - \( 3N \) 个自由度
    - 声学波
      - \( 3 \) 个声学波
    - 光学波
      - \( 3N-3 \) 个光学波
  - 波矢表示
    - 定义
      - \( \mathbf{q} = h_1 \mathbf{b}_1 + h_2 \mathbf{b}_2 + h_3 \mathbf{b}_3 \)
- 振动模式密度
  - 定义
    - \( g(\omega) = \frac{\mathrm{d}N}{\mathrm{d}\omega} \)
  - 计算方法
    - 公式
      - \( \Delta n = \frac{V}{(2\pi)^3} \int_{S(\omega)} \frac{\mathrm{d}s}{|\nabla_q \omega(q)|} \Delta \omega \)
  - 归一化条件
    - \( \int_{0}^{\omega_D} g(\omega) \, \mathrm{d}\omega = 3N \)
- 离子晶体
  - 光频支频率
    - 公式
      - \( \omega = \sqrt{\frac{k(M - m)}{Mm}} \)
- 黄昆方程
  - 方程形式
    - \[
    \begin{cases}
    \displaystyle
    \ddot{W} = b_{11} W + b_{12} E \\
    P = b_{21} W + b_{22} E
    \end{cases}
    \]
  - 系数关系
    - \( b_{11} = -\omega_0^2 \)
    - 频率关系
      - \( \frac{\omega_L^2}{\omega_T^2} = \frac{\varepsilon_s}{\varepsilon_\infty} \)
- 晶体热容
  - 德拜模型
    - 低温热容公式
      - \( C_V = \frac{12\pi^4}{5} R \left( \frac{T}{\theta_D} \right)^3 \)
    - 德拜温度定义
      - \( \theta_D = \frac{h \nu_D}{k_B} \)