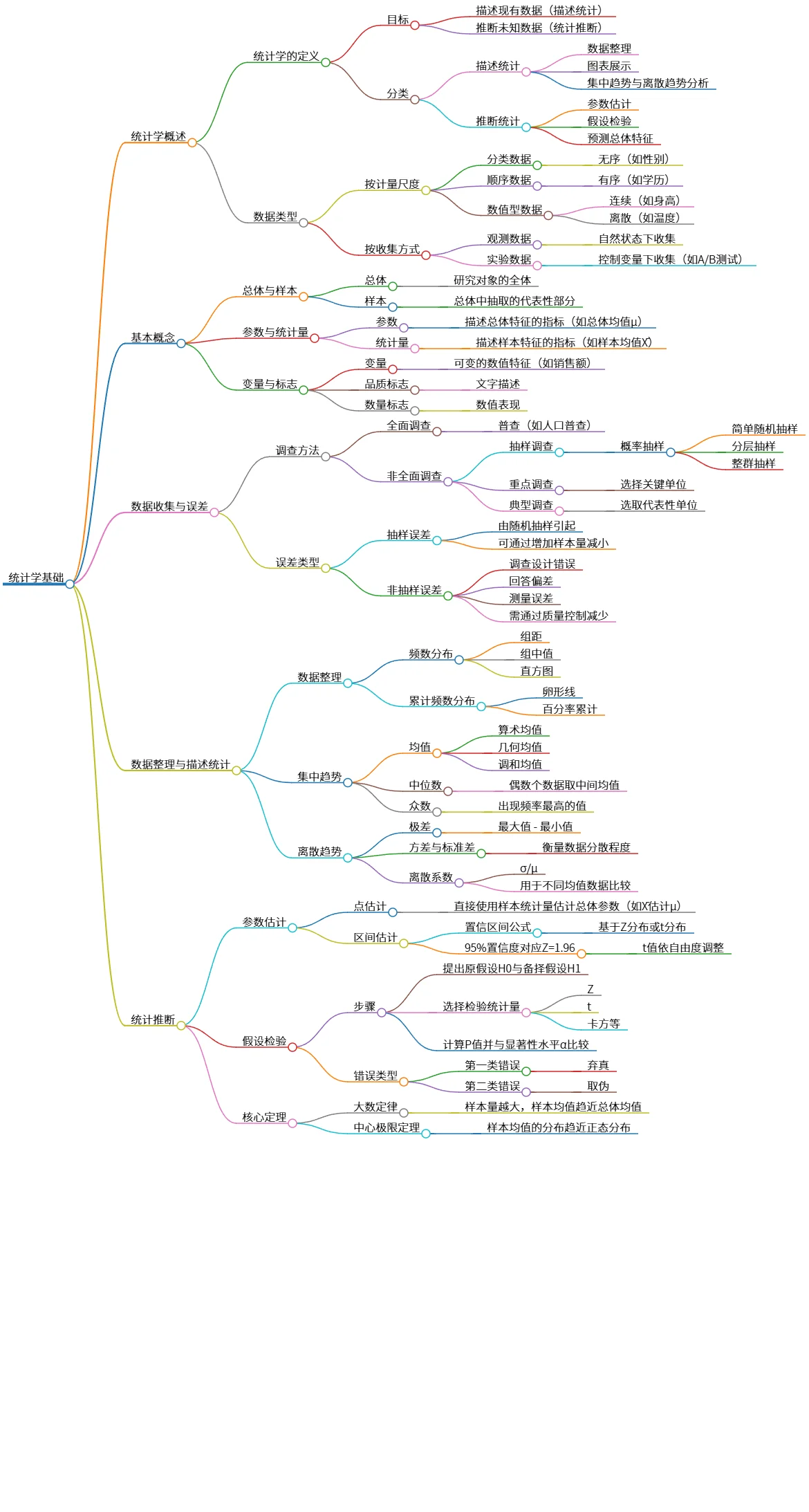
统计学基础：从数据收集到推断与分析方法

# 统计学基础
- 统计学概述
  - 统计学的定义
    - 目标
      - 描述现有数据（描述统计）
      - 推断未知数据（统计推断）
    - 分类
      - 描述统计
        - 数据整理
        - 图表展示
        - 集中趋势与离散趋势分析
      - 推断统计
        - 参数估计
        - 假设检验
        - 预测总体特征
  - 数据类型
    - 按计量尺度
      - 分类数据
        - 无序（如性别）
      - 顺序数据
        - 有序（如学历）
      - 数值型数据
        - 连续（如身高）
        - 离散（如温度）
    - 按收集方式
      - 观测数据
        - 自然状态下收集
      - 实验数据
        - 控制变量下收集（如A/B测试）
- 基本概念
  - 总体与样本
    - 总体
      - 研究对象的全体
    - 样本
      - 总体中抽取的代表性部分
  - 参数与统计量
    - 参数
      - 描述总体特征的指标（如总体均值μ）
    - 统计量
      - 描述样本特征的指标（如样本均值X̄）
  - 变量与标志
    - 变量
      - 可变的数值特征（如销售额）
    - 品质标志
      - 文字描述
    - 数量标志
      - 数值表现
- 数据收集与误差
  - 调查方法
    - 全面调查
      - 普查（如人口普查）
    - 非全面调查
      - 抽样调查
        - 概率抽样
          - 简单随机抽样
          - 分层抽样
          - 整群抽样
      - 重点调查
        - 选择关键单位
      - 典型调查
        - 选取代表性单位
  - 误差类型
    - 抽样误差
      - 由随机抽样引起
      - 可通过增加样本量减小
    - 非抽样误差
      - 调查设计错误
      - 回答偏差
      - 测量误差
      - 需通过质量控制减少
- 数据整理与描述统计
  - 数据整理
    - 频数分布
      - 组距
      - 组中值
      - 直方图
    - 累计频数分布
      - 卵形线
      - 百分率累计
  - 集中趋势
    - 均值
      - 算术均值
      - 几何均值
      - 调和均值
    - 中位数
      - 偶数个数据取中间均值
    - 众数
      - 出现频率最高的值
  - 离散趋势
    - 极差
      - 最大值 - 最小值
    - 方差与标准差
      - 衡量数据分散程度
    - 离散系数
      - σ/μ
      - 用于不同均值数据比较
- 统计推断
  - 参数估计
    - 点估计
      - 直接使用样本统计量估计总体参数（如X̄估计μ）
    - 区间估计
      - 置信区间公式
        - 基于Z分布或t分布
      - 95%置信度对应Z=1.96
        - t值依自由度调整
  - 假设检验
    - 步骤
      - 提出原假设H0与备择假设H1
      - 选择检验统计量
        - Z
        - t
        - 卡方等
      - 计算P值并与显著性水平α比较
    - 错误类型
      - 第一类错误
        - 弃真
      - 第二类错误
        - 取伪
  - 核心定理
    - 大数定律
      - 样本量越大，样本均值趋近总体均值
    - 中心极限定理
      - 样本均值的分布趋近正态分布