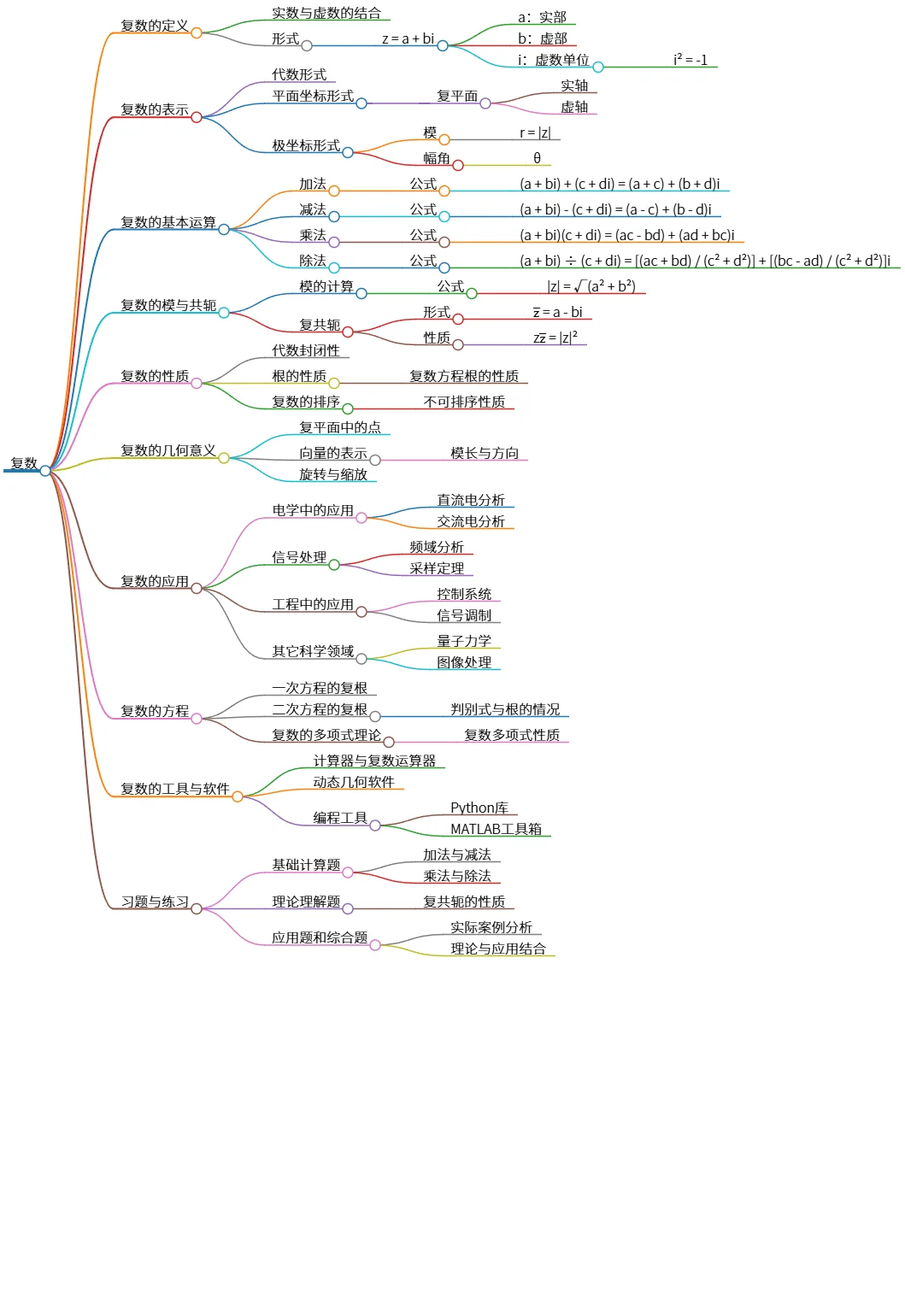
复数的定义、性质与应用：全面解析复数知识

该思维导图系统性地介绍了复数的概念与性质，包括复数的定义、表示形式和基本运算。内容涵盖复数的模与共轭、代数性质、几何意义以及实际应用，如电学与信号处理。此外，复数方程及其根的性质、常用工具和习题也被一一列出，为学习复数提供了全面的指导和练习。

源码

# 复数
- 复数的定义
  - 实数与虚数的结合
  - 形式
    - z = a + bi
      - a：实部
      - b：虚部
      - i：虚数单位
        - i² = -1
- 复数的表示
  - 代数形式
  - 平面坐标形式
    - 复平面
      - 实轴
      - 虚轴
  - 极坐标形式
    - 模
      - r = |z|
    - 幅角
      - θ
- 复数的基本运算
  - 加法
    - 公式
      - (a + bi) + (c + di) = (a + c) + (b + d)i
  - 减法
    - 公式
      - (a + bi) - (c + di) = (a - c) + (b - d)i
  - 乘法
    - 公式
      - (a + bi)(c + di) = (ac - bd) + (ad + bc)i
  - 除法
    - 公式
      - (a + bi) ÷ (c + di) = [(ac + bd) / (c² + d²)] + [(bc - ad) / (c² + d²)]i
- 复数的模与共轭
  - 模的计算
    - 公式
      - |z| = √(a² + b²)
  - 复共轭
    - 形式
      - z̅ = a - bi
    - 性质
      - zz̅ = |z|²
- 复数的性质
  - 代数封闭性
  - 根的性质
    - 复数方程根的性质
  - 复数的排序
    - 不可排序性质
- 复数的几何意义
  - 复平面中的点
  - 向量的表示
    - 模长与方向
  - 旋转与缩放
- 复数的应用
  - 电学中的应用
    - 直流电分析
    - 交流电分析
  - 信号处理
    - 频域分析
    - 采样定理
  - 工程中的应用
    - 控制系统
    - 信号调制
  - 其它科学领域
    - 量子力学
    - 图像处理
- 复数的方程
  - 一次方程的复根
  - 二次方程的复根
    - 判别式与根的情况
  - 复数的多项式理论
    - 复数多项式性质
- 复数的工具与软件
  - 计算器与复数运算器
  - 动态几何软件
  - 编程工具
    - Python库
    - MATLAB工具箱
- 习题与练习
  - 基础计算题
    - 加法与减法
    - 乘法与除法
  - 理论理解题
    - 复共轭的性质
  - 应用题和综合题
    - 实际案例分析
    - 理论与应用结合

图片