圆锥曲线知识点整理与解题技巧探讨
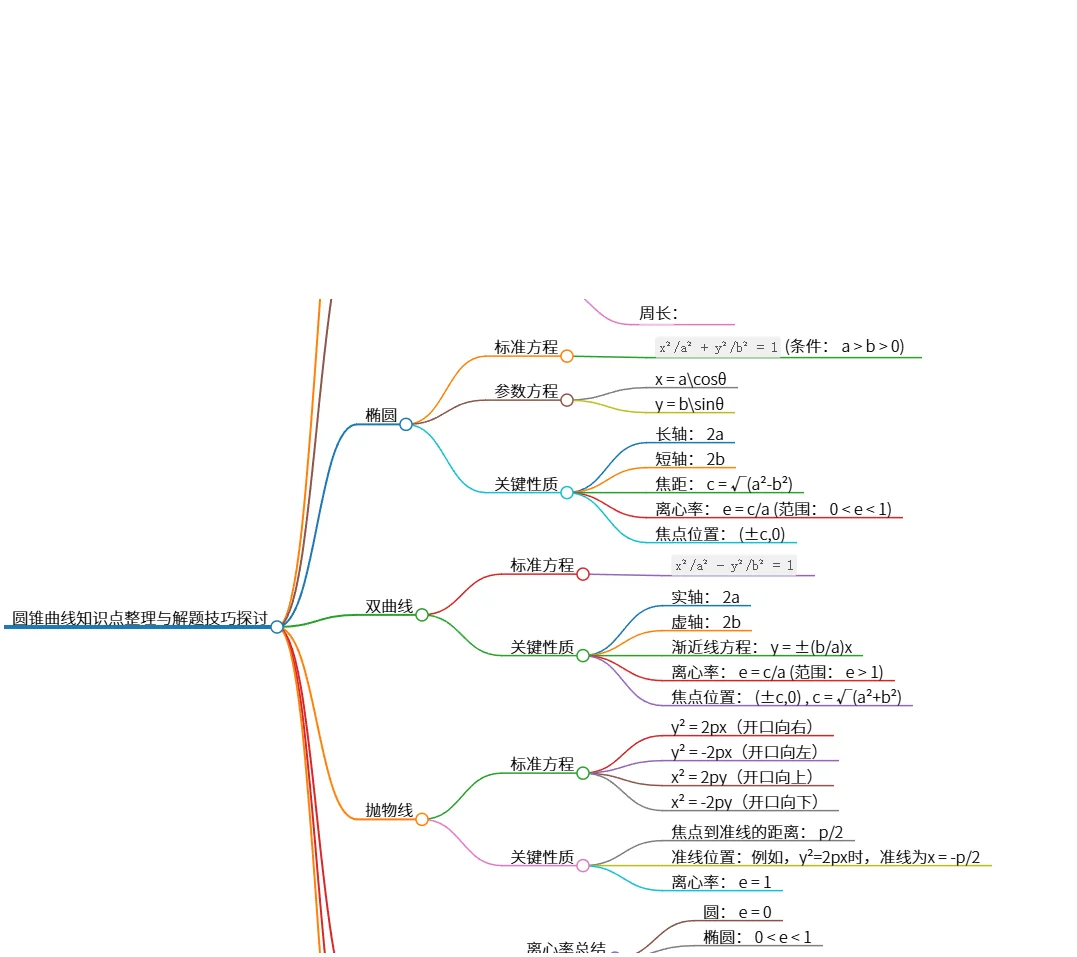
该思维导图整理了圆锥曲线的基本概念、分类及其性质,包括圆、椭圆、双曲线和抛物线的标准方程、参数方程及关键性质。此外,介绍了离心率的统一性质、准线和焦点性质,并列出了相关重要公式与解题技巧,强调几何与代数结合的重要性,为学习和理解圆锥曲线提供了系统性指导。
源码
# 圆锥曲线知识点整理与解题技巧探讨
- 基本概念
- 定义
- 平面与圆锥面相交产生的曲线
- 分类
- 圆
- 椭圆
- 双曲线
- 抛物线
- 圆
- 标准方程
- `(x-a)² + (y-b)² = r²`
- 参数方程
- x = a + r\cosθ
- y = b + r\sinθ
- 关键性质
- 圆心: (a,b)
- 半径: r
- 对称性: 关于任意直径对称
- 周长: `2πr`
- 椭圆
- 标准方程
- `x²/a² + y²/b² = 1` (条件: a > b > 0)
- 参数方程
- x = a\cosθ
- y = b\sinθ
- 关键性质
- 长轴: 2a
- 短轴: 2b
- 焦距: c = √(a²-b²)
- 离心率: e = c/a (范围: 0 < e < 1)
- 焦点位置: (±c,0)
- 双曲线
- 标准方程
- `x²/a² - y²/b² = 1`
- 关键性质
- 实轴: 2a
- 虚轴: 2b
- 渐近线方程: y = ±(b/a)x
- 离心率: e = c/a (范围: e > 1)
- 焦点位置: (±c,0) , c = √(a²+b²)
- 抛物线
- 标准方程
- y² = 2px(开口向右)
- y² = -2px(开口向左)
- x² = 2py(开口向上)
- x² = -2py(开口向下)
- 关键性质
- 焦点到准线的距离: p/2
- 准线位置:例如,y²=2px时,准线为x = -p/2
- 离心率: e = 1
- 统一性质
- 离心率总结
- 圆: e = 0
- 椭圆: 0 < e < 1
- 抛物线: e = 1
- 双曲线: e > 1
- 准线特点
- 所有圆锥曲线都有准线
- 焦点的反射性质
- 光学反射原理
- 重要公式
- 切线方程(椭圆特例)
- `xx₀/a² + yy₀/b² = 1` ((x₀,y₀)为切点)
- 弦长公式
- `L = √(1+k²)|x₁-x₂|` (k为斜率)
- 解题技巧
- 明确定义
- 理解各种曲线的特性
- 几何与代数结合
- 用代数公式解决几何问题
- 参数方程应用
- 在特定情境中使用参数方程简化计算
- 特殊情况考虑
- 识别退化的圆锥曲线如点、直线
图片