频域分析法基础与Nyquist判据及Bode图分析

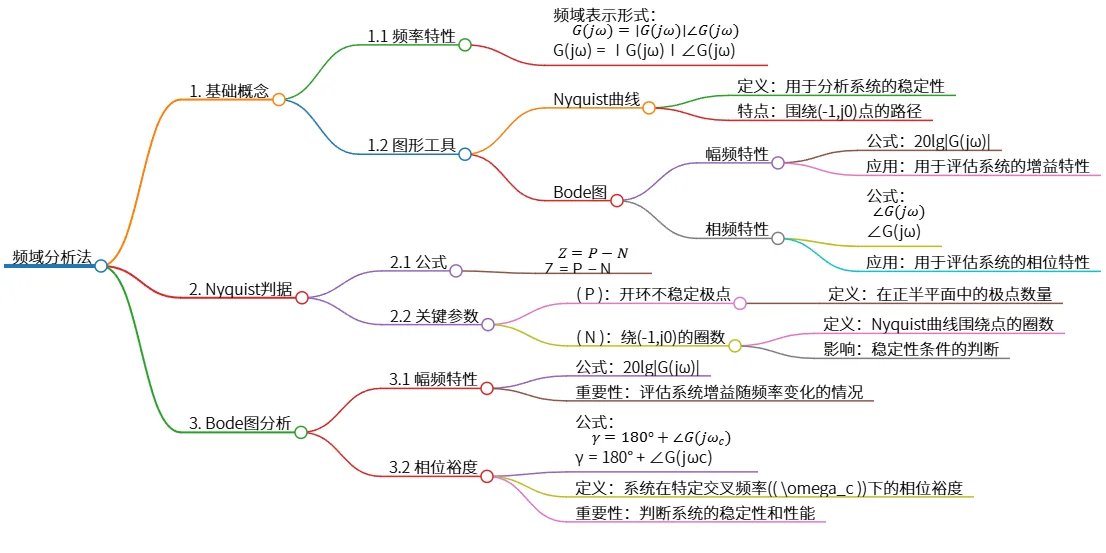
该思维导图概述了频域分析法的基础概念，包括频率特性及图形工具如Nyquist曲线和Bode图。重点描述了Nyquist判据，公式为\( Z = P - N \)，其中\( P \)表示开环不稳定极点，\( N \)为绕(-1,j0)的圈数。此外，Bode图分析部分介绍了幅频特性和相位裕度计算，幅频特性为20lg|G(jω)|，相位裕度公式为\( \gamma = 180° + \angle G(j\omega_c) \)。

源码

# 频域分析法
## 1. 基础概念
### 1.1 频率特性
- 频域表示形式：$$ G(j\omega) = |G(j\omega)| \angle G(j\omega) $$
### 1.2 图形工具
- Nyquist曲线
  - 定义：用于分析系统的稳定性
  - 特点：围绕(-1,j0)点的路径
- Bode图
  - 幅频特性
    - 公式：20lg|G(jω)|
    - 应用：用于评估系统的增益特性
  - 相频特性
    - 公式：$$ \angle G(j\omega) $$
    - 应用：用于评估系统的相位特性
## 2. Nyquist判据
### 2.1 公式
- $$ Z = P - N $$
### 2.2 关键参数
- \( P \)：开环不稳定极点
  - 定义：在正半平面中的极点数量
- \( N \)：绕(-1,j0)的圈数
  - 定义：Nyquist曲线围绕点的圈数
  - 影响：稳定性条件的判断
## 3. Bode图分析
### 3.1 幅频特性
- 公式：20lg|G(jω)|
- 重要性：评估系统增益随频率变化的情况
### 3.2 相位裕度
- 公式：$$ \gamma = 180° + \angle G(j\omega_c) $$
- 定义：系统在特定交叉频率(\( \omega_c \))下的相位裕度
- 重要性：判断系统的稳定性和性能

图片