毕奥-萨伐尔定律及其在电磁学中的应用与联系
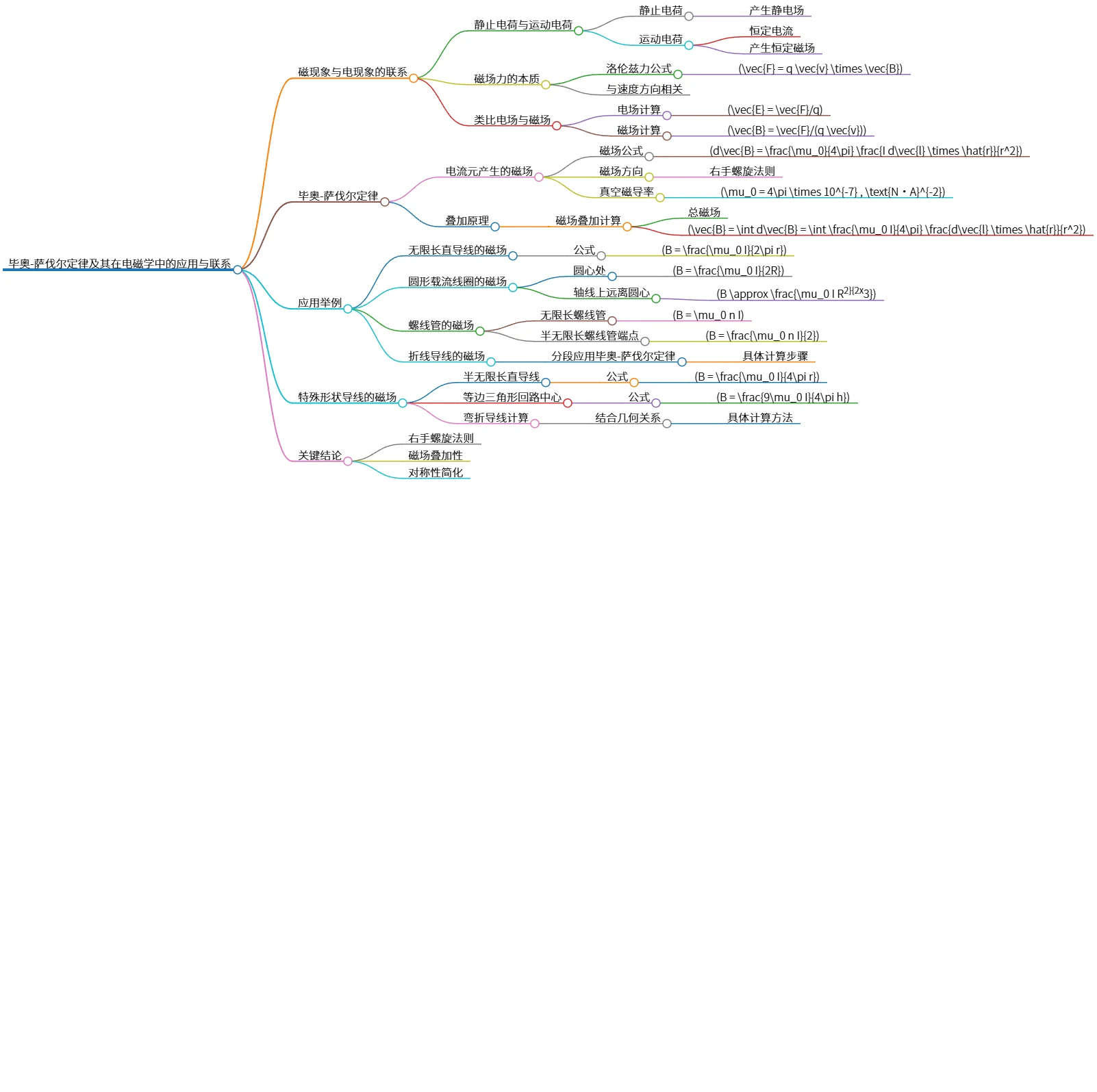
该思维导图介绍了毕奥-萨伐尔定律及其相关概念,阐述了静止电荷与运动电荷的区别、磁场力的本质和计算方法。定律内容包括电流元产生的磁场公式、叠加原理及其应用实例,如无限长直导线、圆形载流线圈和螺线管的磁场计算。同时讨论特殊形状导线的磁场。强调了右手螺旋法则、磁场的叠加性和对称性简化的重要性。
源码
# 毕奥-萨伐尔定律及其在电磁学中的应用与联系
- 磁现象与电现象的联系
- 静止电荷与运动电荷
- 静止电荷
- 产生静电场
- 运动电荷
- 恒定电流
- 产生恒定磁场
- 磁场力的本质
- 洛伦兹力公式
- \(\vec{F} = q \vec{v} \times \vec{B}\)
- 与速度方向相关
- 类比电场与磁场
- 电场计算
- \(\vec{E} = \vec{F}/q\)
- 磁场计算
- \(\vec{B} = \vec{F}/(q \vec{v})\)
- 毕奥-萨伐尔定律
- 电流元产生的磁场
- 磁场公式
- \(d\vec{B} = \frac{\mu_0}{4\pi} \frac{I d\vec{l} \times \hat{r}}{r^2}\)
- 磁场方向
- 右手螺旋法则
- 真空磁导率
- \(\mu_0 = 4\pi \times 10^{-7} \, \text{N·A}^{-2}\)
- 叠加原理
- 磁场叠加计算
- 总磁场
- \(\vec{B} = \int d\vec{B} = \int \frac{\mu_0 I}{4\pi} \frac{d\vec{l} \times \hat{r}}{r^2}\)
- 应用举例
- 无限长直导线的磁场
- 公式
- \(B = \frac{\mu_0 I}{2\pi r}\)
- 圆形载流线圈的磁场
- 圆心处
- \(B = \frac{\mu_0 I}{2R}\)
- 轴线上远离圆心
- \(B \approx \frac{\mu_0 I R^2}{2x^3}\)
- 螺线管的磁场
- 无限长螺线管
- \(B = \mu_0 n I\)
- 半无限长螺线管端点
- \(B = \frac{\mu_0 n I}{2}\)
- 折线导线的磁场
- 分段应用毕奥-萨伐尔定律
- 具体计算步骤
- 特殊形状导线的磁场
- 半无限长直导线
- 公式
- \(B = \frac{\mu_0 I}{4\pi r}\)
- 等边三角形回路中心
- 公式
- \(B = \frac{9\mu_0 I}{4\pi h}\)
- 弯折导线计算
- 结合几何关系
- 具体计算方法
- 关键结论
- 右手螺旋法则
- 磁场叠加性
- 对称性简化
图片