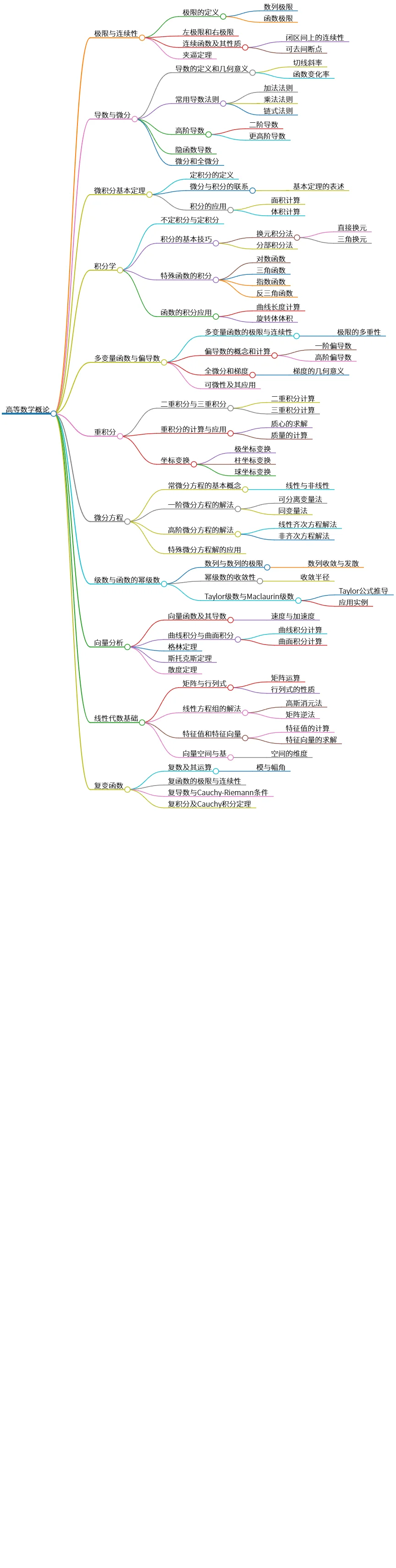
高等数学概论：极限、导数、积分与微分方程应用

# 高等数学概论
- 极限与连续性
  - 极限的定义
    - 数列极限
    - 函数极限
  - 左极限和右极限
  - 连续函数及其性质
    - 闭区间上的连续性
    - 可去间断点
  - 夹逼定理
- 导数与微分
  - 导数的定义和几何意义
    - 切线斜率
    - 函数变化率
  - 常用导数法则
    - 加法法则
    - 乘法法则
    - 链式法则
  - 高阶导数
    - 二阶导数
    - 更高阶导数
  - 隐函数导数
  - 微分和全微分
- 微积分基本定理
  - 定积分的定义
  - 微分与积分的联系
    - 基本定理的表述
  - 积分的应用
    - 面积计算
    - 体积计算
- 积分学
  - 不定积分与定积分
  - 积分的基本技巧
    - 换元积分法
      - 直接换元
      - 三角换元
    - 分部积分法
  - 特殊函数的积分
    - 对数函数
    - 三角函数
    - 指数函数
    - 反三角函数
  - 函数的积分应用
    - 曲线长度计算
    - 旋转体体积
- 多变量函数与偏导数
  - 多变量函数的极限与连续性
    - 极限的多重性
  - 偏导数的概念和计算
    - 一阶偏导数
    - 高阶偏导数
  - 全微分和梯度
    - 梯度的几何意义
  - 可微性及其应用
- 重积分
  - 二重积分与三重积分
    - 二重积分计算
    - 三重积分计算
  - 重积分的计算与应用
    - 质心的求解
    - 质量的计算
  - 坐标变换
    - 极坐标变换
    - 柱坐标变换
    - 球坐标变换
- 微分方程
  - 常微分方程的基本概念
    - 线性与非线性
  - 一阶微分方程的解法
    - 可分离变量法
    - 同变量法
  - 高阶微分方程的解法
    - 线性齐次方程解法
    - 非齐次方程解法
  - 特殊微分方程解的应用
- 级数与函数的幂级数
  - 数列与数列的极限
    - 数列收敛与发散
  - 幂级数的收敛性
    - 收敛半径
  - Taylor级数与Maclaurin级数
    - Taylor公式推导
    - 应用实例
- 向量分析
  - 向量函数及其导数
    - 速度与加速度
  - 曲线积分与曲面积分
    - 曲线积分计算
    - 曲面积分计算
  - 格林定理
  - 斯托克斯定理
  - 散度定理
- 线性代数基础
  - 矩阵与行列式
    - 矩阵运算
    - 行列式的性质
  - 线性方程组的解法
    - 高斯消元法
    - 矩阵逆法
  - 特征值和特征向量
    - 特征值的计算
    - 特征向量的求解
  - 向量空间与基
    - 空间的维度
- 复变函数
  - 复数及其运算
    - 模与幅角
  - 复函数的极限与连续性
  - 复导数与Cauchy-Riemann条件
  - 复积分及Cauchy积分定理