电路分析方法与应用实例概述与技巧
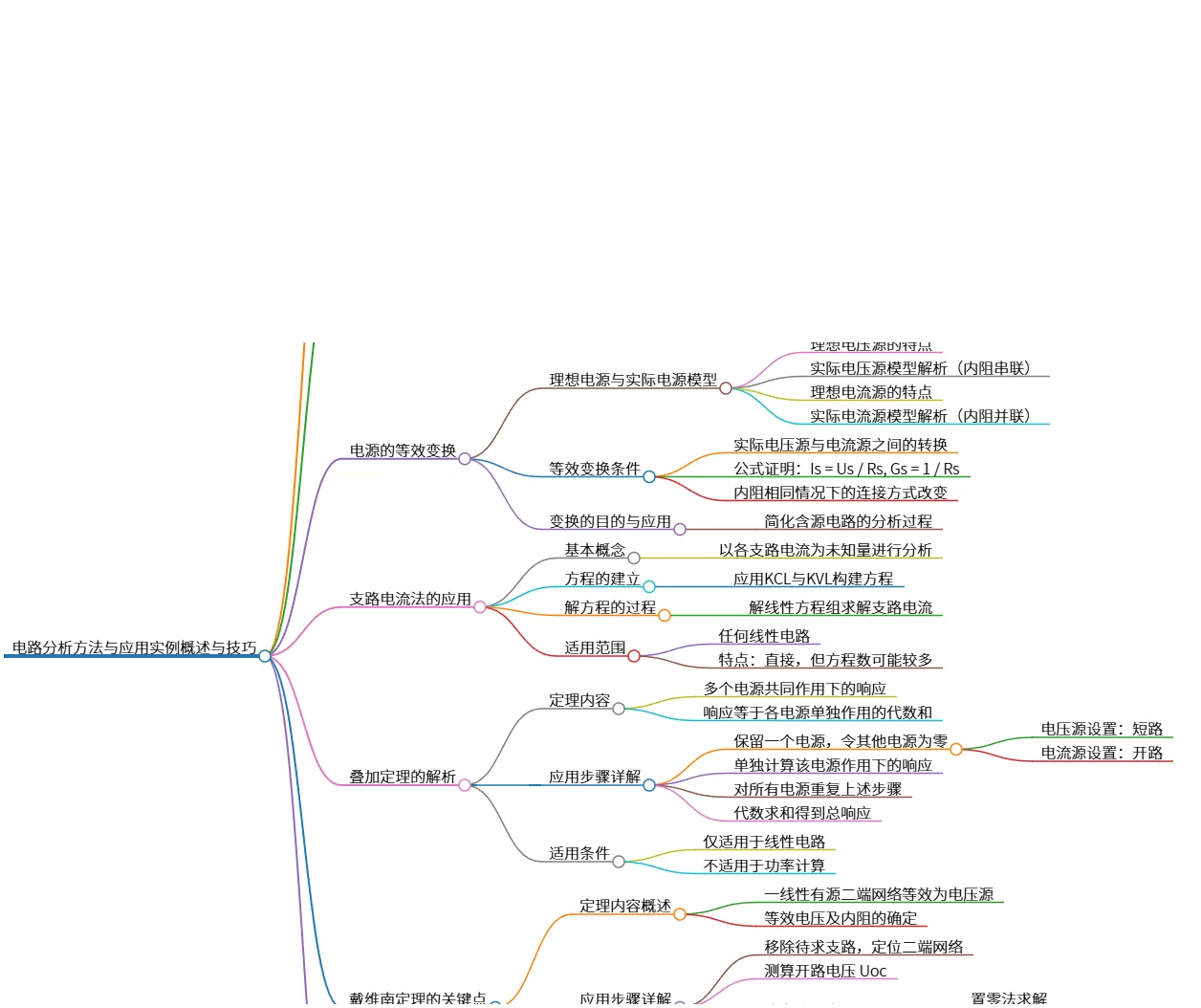
该思维导图概述了电路分析的基本方法,包括二端网络及其等效概念,电阻的串联、并联及混联,电源的等效变换,支路电流法、叠加定理和戴维南定理。每个方法的基本思想、应用步骤及适用范围均有所介绍,如戴维南定理可简化复杂网络,并适用于电路设计和故障诊断。整体内容为电路分析提供系统性指导,助于理解和解决实际电路问题。
源码
# 电路分析方法与应用实例概述与技巧
- 电路分析的基本概念
- 二端网络的定义与特性
- 二端网络定义
- 端口特性说明
- 等效概念的引入
- 等效条件的理解
- 目的:简化电路分析
- 电阻的连接方式
- 串联电阻
- 特点:电流相同
- 等效电阻计算:Req = R1 + R2 + ... + Rn
- 分压公式:Uk = (Rk / Req) * U
- 并联电阻
- 特点:电压相同
- 等效电阻计算:1/Req = 1/R1 + 1/R2 + ... + 1/Rn
- 分流公式:Ik = (Req / Rk) * I
- 混联电阻
- 定义:串并联组合
- 分析方法:逐步等效化简
- 电源的等效变换
- 理想电源与实际电源模型
- 理想电压源的特点
- 实际电压源模型解析(内阻串联)
- 理想电流源的特点
- 实际电流源模型解析(内阻并联)
- 等效变换条件
- 实际电压源与电流源之间的转换
- 公式证明:Is = Us / Rs, Gs = 1 / Rs
- 内阻相同情况下的连接方式改变
- 变换的目的与应用
- 简化含源电路的分析过程
- 支路电流法的应用
- 基本概念
- 以各支路电流为未知量进行分析
- 方程的建立
- 应用KCL与KVL构建方程
- 解方程的过程
- 解线性方程组求解支路电流
- 适用范围
- 任何线性电路
- 特点:直接,但方程数可能较多
- 叠加定理的解析
- 定理内容
- 多个电源共同作用下的响应
- 响应等于各电源单独作用的代数和
- 应用步骤详解
- 保留一个电源,令其他电源为零
- 电压源设置:短路
- 电流源设置:开路
- 单独计算该电源作用下的响应
- 对所有电源重复上述步骤
- 代数求和得到总响应
- 适用条件
- 仅适用于线性电路
- 不适用于功率计算
- 戴维南定理的关键点
- 定理内容概述
- 一线性有源二端网络等效为电压源
- 等效电压及内阻的确定
- 应用步骤详解
- 移除待求支路,定位二端网络
- 测算开路电压 Uoc
- 确定等效内阻 Ro
- 置零法求解
- 开路短路法求解:Ro = Uoc / Isc
- 绘制等效电路,接入待求支路进行求解
- 目的与优势
- 简化复杂电路分析
- 特别适合单一支路变化分析
- 应用实例与问题解决
- 综合应用
- 结合等效化简与电源变换
- 结合支路法与叠加定理
- 结合戴维南定理进行分析
- 典型电路分析实例
- 含受控源的电路
- 桥式电路的分析技巧
- 最大功率传输问题探讨
- 实际问题的解决策略
- 电路设计的方法论
- 故障诊断的具体步骤
- 性能优化的实践经验
图片