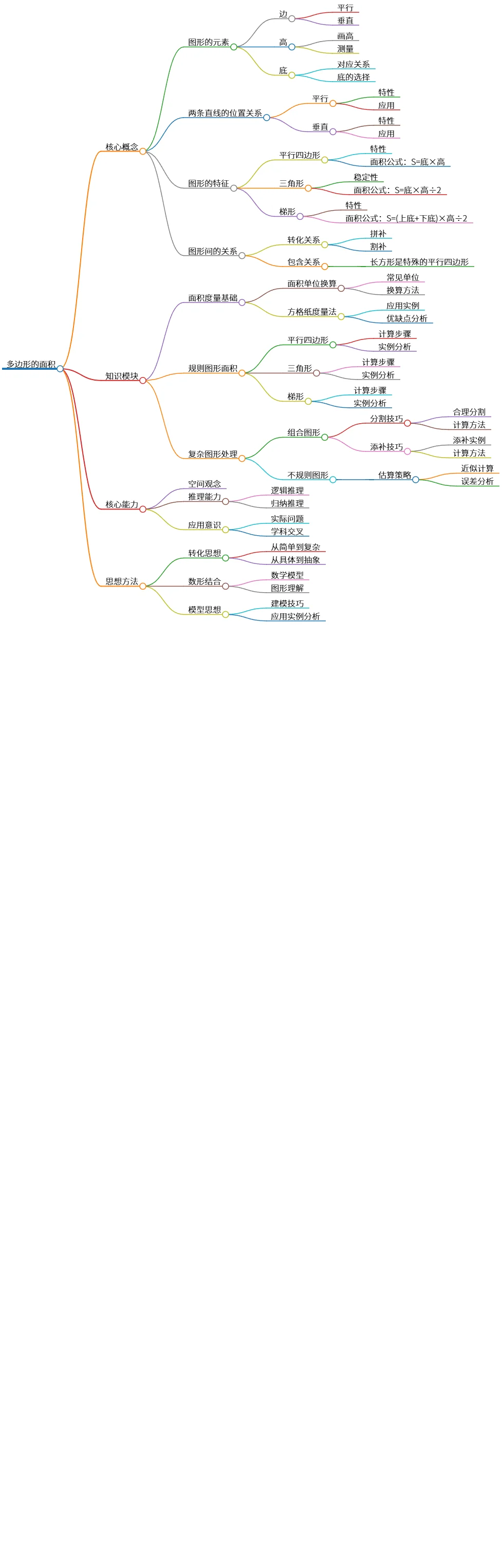
多边形的面积及其计算方法与思维方式解析

该思维导图概括了多边形面积的核心概念、知识模块、核心能力和思想方法。核心概念包括图形元素、两条直线的位置关系及图形特征，知识模块涵盖面积度量基础、规则图形面积计算和复杂图形处理技巧。核心能力强调空间观念、推理能力和应用意识。思想方法则包含转化思想、数形结合和模型思想，为学生理解和应用多边形面积的计算提供了全面的指导。

源码

# 多边形的面积
- 核心概念
  - 图形的元素
    - 边
      - 平行
      - 垂直
    - 高
      - 画高
      - 测量
    - 底
      - 对应关系
      - 底的选择
  - 两条直线的位置关系
    - 平行
      - 特性
      - 应用
    - 垂直
      - 特性
      - 应用
  - 图形的特征
    - 平行四边形
      - 特性
      - 面积公式：S=底×高
    - 三角形
      - 稳定性
      - 面积公式：S=底×高÷2
    - 梯形
      - 特性
      - 面积公式：S=(上底+下底)×高÷2
  - 图形间的关系
    - 转化关系
      - 拼补
      - 割补
    - 包含关系
      - 长方形是特殊的平行四边形
- 知识模块
  - 面积度量基础
    - 面积单位换算
      - 常见单位
      - 换算方法
    - 方格纸度量法
      - 应用实例
      - 优缺点分析
  - 规则图形面积
    - 平行四边形
      - 计算步骤
      - 实例分析
    - 三角形
      - 计算步骤
      - 实例分析
    - 梯形
      - 计算步骤
      - 实例分析
  - 复杂图形处理
    - 组合图形
      - 分割技巧
        - 合理分割
        - 计算方法
      - 添补技巧
        - 添补实例
        - 计算方法
    - 不规则图形
      - 估算策略
        - 近似计算
        - 误差分析
- 核心能力
  - 空间观念
  - 推理能力
    - 逻辑推理
    - 归纳推理
  - 应用意识
    - 实际问题
    - 学科交叉
- 思想方法
  - 转化思想
    - 从简单到复杂
    - 从具体到抽象
  - 数形结合
    - 数学模型
    - 图形理解
  - 模型思想
    - 建模技巧
    - 应用实例分析

图片