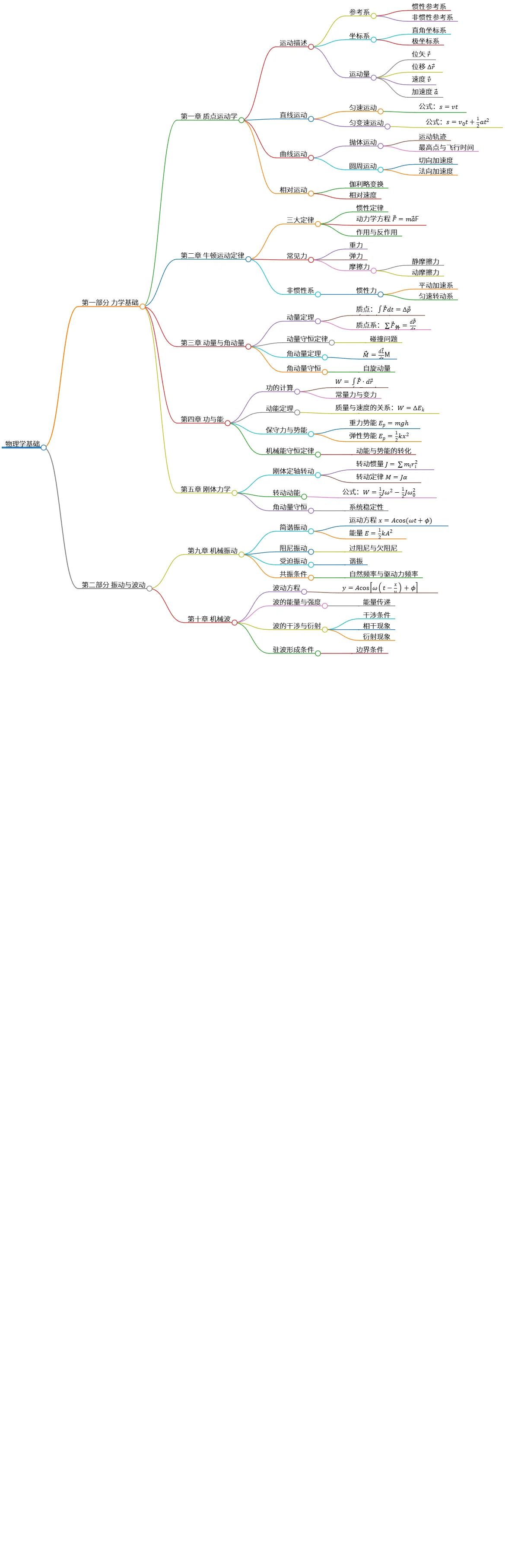
物理学基础：力学、振动与波动的关键概念与定律

# 物理学基础
- 第一部分 力学基础
  - 第一章 质点运动学
    - 运动描述
      - 参考系
        - 惯性参考系
        - 非惯性参考系
      - 坐标系
        - 直角坐标系
        - 极坐标系
      - 运动量
        - 位矢 $\vec{r}$
        - 位移 $\Delta\vec{r}$
        - 速度 $\vec{v}$
        - 加速度 $\vec{a}$
    - 直线运动
      - 匀速运动
        - 公式：$s = vt$
      - 匀变速运动
        - 公式：$s = v_0t + \frac{1}{2}at^2$
    - 曲线运动
      - 抛体运动
        - 运动轨迹
        - 最高点与飞行时间
      - 圆周运动
        - 切向加速度
        - 法向加速度
    - 相对运动
      - 伽利略变换
      - 相对速度
  - 第二章 牛顿运动定律
    - 三大定律
      - 惯性定律
      - 动力学方程 $\vec{F}=m\vec{a}$
      - 作用与反作用
    - 常见力
      - 重力
      - 弹力
      - 摩擦力
        - 静摩擦力
        - 动摩擦力
    - 非惯性系
      - 惯性力
        - 平动加速系
        - 匀速转动系
  - 第三章 动量与角动量
    - 动量定理
      - 质点：$\int \vec{F}dt = \Delta\vec{p}$
      - 质点系：$\sum\vec{F}_{外} = \frac{d\vec{P}}{dt}$
    - 动量守恒定律
      - 碰撞问题
    - 角动量定理
      - $\vec{M} = \frac{d\vec{L}}{dt}$
    - 角动量守恒
      - 自旋动量
  - 第四章 功与能
    - 功的计算
      - $W = \int \vec{F} \cdot d\vec{r}$
      - 常量力与变力
    - 动能定理
      - 质量与速度的关系：$W = \Delta E_k$
    - 保守力与势能
      - 重力势能 $E_p = mgh$
      - 弹性势能 $E_p = \frac{1}{2}kx^2$
    - 机械能守恒定律
      - 动能与势能的转化
  - 第五章 刚体力学
    - 刚体定轴转动
      - 转动惯量 $J = \sum m_i r_i^2$
      - 转动定律 $M = J\alpha$
    - 转动动能
      - 公式：$W = \frac{1}{2}J\omega^2 - \frac{1}{2}J\omega_0^2$
    - 角动量守恒
      - 系统稳定性
- 第二部分 振动与波动
  - 第九章 机械振动
    - 简谐振动
      - 运动方程 $x = A\cos(\omega t + \phi)$
      - 能量 $E = \frac{1}{2}kA^2$
    - 阻尼振动
      - 过阻尼与欠阻尼
    - 受迫振动
      - 谐振
    - 共振条件
      - 自然频率与驱动力频率
  - 第十章 机械波
    - 波动方程
      - $y = A\cos\left[\omega\left(t - \frac{x}{u}\right) + \phi\right]$
    - 波的能量与强度
      - 能量传递
    - 波的干涉与衍射
      - 干涉条件
      - 相干现象
      - 衍射现象
    - 驻波形成条件
      - 边界条件