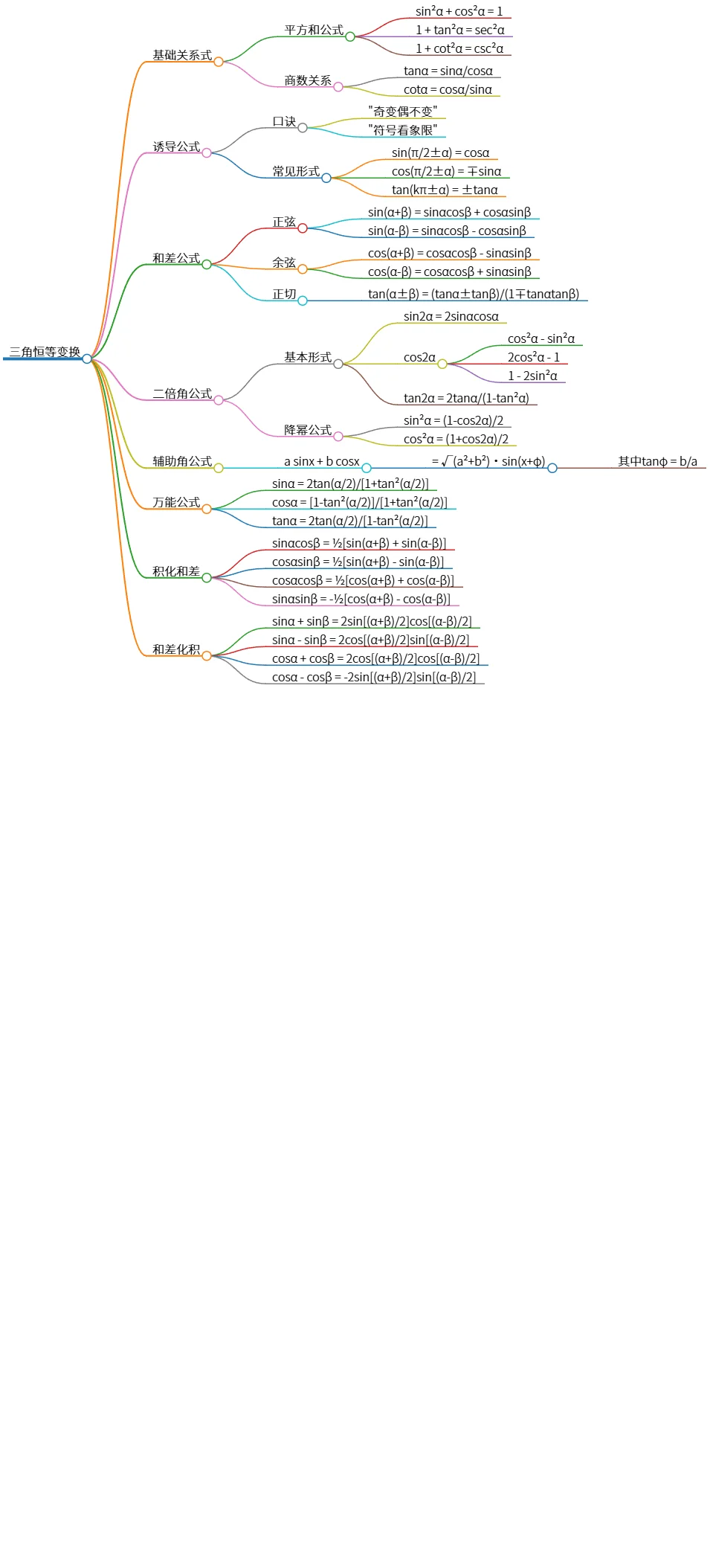
三角恒等变换与基础公式的全面总结与应用

该思维导图总结了三角恒等变换的基础关系式、诱导公式、和差公式、二倍角公式、辅助角公式、万能公式、积化和差及和差化积等重要内容，涵盖了三角函数之间的关系及其转换方法，为解题提供了有效的工具和技巧。通过掌握这些公式，可以更好地应用于数学分析及物理问题中。

源码

# 三角恒等变换
- 基础关系式
  - 平方和公式
    - sin²α + cos²α = 1
    - 1 + tan²α = sec²α
    - 1 + cot²α = csc²α
  - 商数关系
    - tanα = sinα/cosα
    - cotα = cosα/sinα
- 诱导公式
  - 口诀
    - "奇变偶不变"
    - "符号看象限"
  - 常见形式
    - sin(π/2±α) = cosα
    - cos(π/2±α) = ∓sinα
    - tan(kπ±α) = ±tanα
- 和差公式
  - 正弦
    - sin(α+β) = sinαcosβ + cosαsinβ
    - sin(α-β) = sinαcosβ - cosαsinβ
  - 余弦
    - cos(α+β) = cosαcosβ - sinαsinβ
    - cos(α-β) = cosαcosβ + sinαsinβ
  - 正切
    - tan(α±β) = (tanα±tanβ)/(1∓tanαtanβ)
- 二倍角公式
  - 基本形式
    - sin2α = 2sinαcosα
    - cos2α
      - cos²α - sin²α
      - 2cos²α - 1
      - 1 - 2sin²α
    - tan2α = 2tanα/(1-tan²α)
  - 降幂公式
    - sin²α = (1-cos2α)/2
    - cos²α = (1+cos2α)/2
- 辅助角公式
  - a sinx + b cosx
    - = √(a²+b²)·sin(x+φ)
      - 其中tanφ = b/a
- 万能公式
  - sinα = 2tan(α/2)/[1+tan²(α/2)]
  - cosα = [1-tan²(α/2)]/[1+tan²(α/2)]
  - tanα = 2tan(α/2)/[1-tan²(α/2)]
- 积化和差
  - sinαcosβ = ½[sin(α+β) + sin(α-β)]
  - cosαsinβ = ½[sin(α+β) - sin(α-β)]
  - cosαcosβ = ½[cos(α+β) + cos(α-β)]
  - sinαsinβ = -½[cos(α+β) - cos(α-β)]
- 和差化积
  - sinα + sinβ = 2sin[(α+β)/2]cos[(α-β)/2]
  - sinα - sinβ = 2cos[(α+β)/2]sin[(α-β)/2]
  - cosα + cosβ = 2cos[(α+β)/2]cos[(α-β)/2]
  - cosα - cosβ = -2sin[(α+β)/2]sin[(α-β)/2]

图片