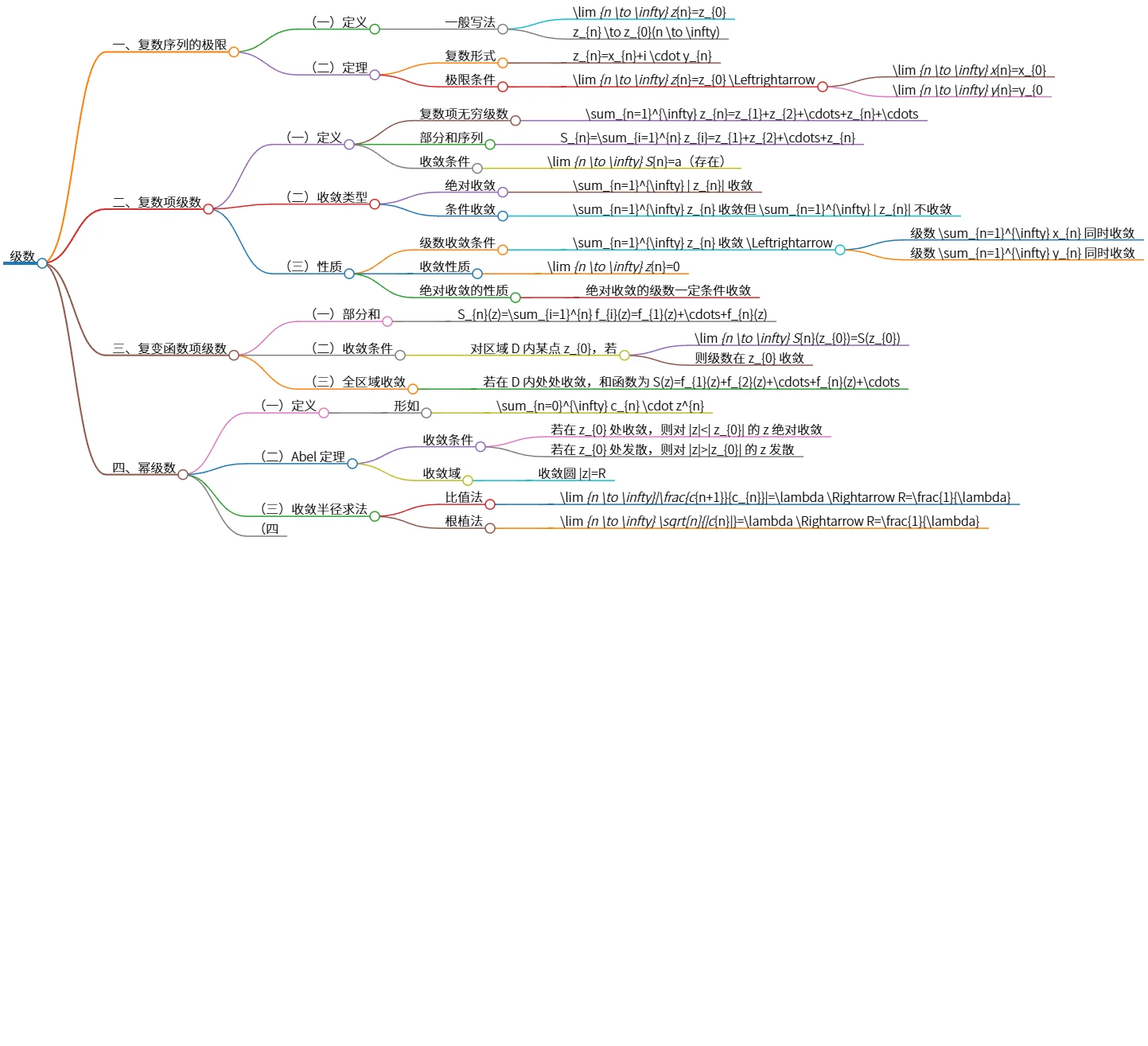
复数序列与级数的极限与展开性质分析

该思维导图概述了复数序列及级数的极限定义、复数项级数的收敛性质、复变函数项级数的收敛情况，以及幂级数的定义和收敛半径的求法。还包括泰勒展开的公式和常用式，以及洛朗展开及其性质、定理与应用。整体内容深入探讨了复数分析中的重要概念，适用于理解级数的收敛性及其在复变函数中的应用。

源码

# 级数
- 一、复数序列的极限
  - （一）定义
    - 一般写法
      - \lim _{n \to \infty} z_{n}=z_{0}
      - z_{n} \to z_{0}(n \to \infty)
  - （二）定理
    - 复数形式
      - z_{n}=x_{n}+i \cdot y_{n}
    - 极限条件
      - \lim _{n \to \infty} z_{n}=z_{0} \Leftrightarrow 
        - \lim _{n \to \infty} x_{n}=x_{0}
        - \lim _{n \to \infty} y_{n}=y_{0
- 二、复数项级数
  - （一）定义
    - 复数项无穷级数
      - \sum_{n=1}^{\infty} z_{n}=z_{1}+z_{2}+\cdots+z_{n}+\cdots
    - 部分和序列
      - S_{n}=\sum_{i=1}^{n} z_{i}=z_{1}+z_{2}+\cdots+z_{n}
    - 收敛条件
      - \lim _{n \to \infty} S_{n}=a（存在）
  - （二）收敛类型
    - 绝对收敛
      - \sum_{n=1}^{\infty} | z_{n}| 收敛
    - 条件收敛
      - \sum_{n=1}^{\infty} z_{n} 收敛但 \sum_{n=1}^{\infty} | z_{n}| 不收敛
  - （三）性质
    - 级数收敛条件
      - \sum_{n=1}^{\infty} z_{n} 收敛 \Leftrightarrow 
        - 级数 \sum_{n=1}^{\infty} x_{n} 同时收敛
        - 级数 \sum_{n=1}^{\infty} y_{n} 同时收敛
    - 收敛性质
      - \lim _{n \to \infty} z_{n}=0
    - 绝对收敛的性质
      - 绝对收敛的级数一定条件收敛
- 三、复变函数项级数
  - （一）部分和
    - S_{n}(z)=\sum_{i=1}^{n} f_{i}(z)=f_{1}(z)+\cdots+f_{n}(z)
  - （二）收敛条件
    - 对区域 D 内某点 z_{0}，若 
      - \lim _{n \to \infty} S_{n}(z_{0})=S(z_{0})
      - 则级数在 z_{0} 收敛
  - （三）全区域收敛
    - 若在 D 内处处收敛，和函数为 S(z)=f_{1}(z)+f_{2}(z)+\cdots+f_{n}(z)+\cdots
- 四、幂级数
  - （一）定义
    - 形如 
      - \sum_{n=0}^{\infty} c_{n} \cdot z^{n}
  - （二）Abel 定理
    - 收敛条件
      - 若在 z_{0} 处收敛，则对 |z|<| z_{0}| 的 z 绝对收敛
      - 若在 z_{0} 处发散，则对 |z|>|z_{0}| 的 z 发散
    - 收敛域
      - 收敛圆 |z|=R
  - （三）收敛半径求法
    - 比值法
      - \lim _{n \to \infty}|\frac{c_{n+1}}{c_{n}}|=\lambda \Rightarrow R=\frac{1}{\lambda}
    - 根植法
      - \lim _{n \to \infty} \sqrt[n]{|c_{n}|}=\lambda \Rightarrow R=\frac{1}{\lambda}
  - （四

图片