高等数学:函数、极限、导数与应用的深入探讨
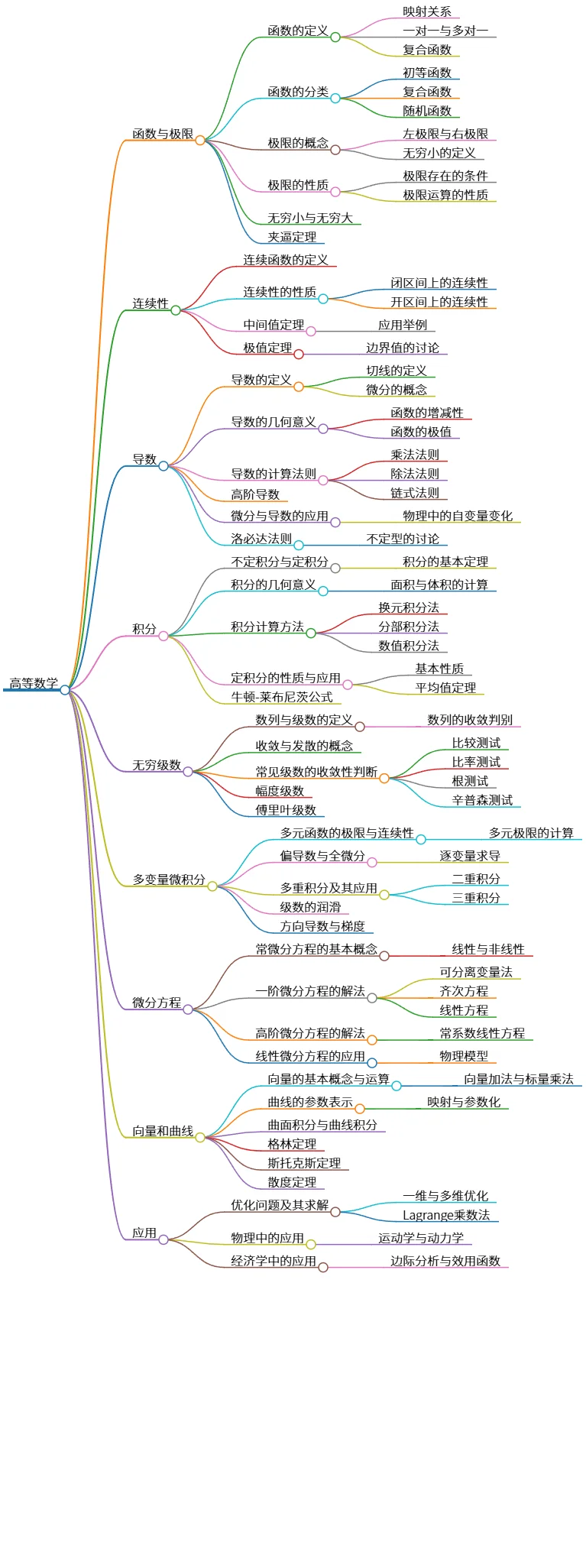
该思维导图概述了高等数学的主要内容,包括函数与极限、连续性、导数、积分、无穷级数、多变量微积分、微分方程、向量和曲线及其应用。重点涵盖了极限的概念及性质、导数的几何意义及计算法则、定积分以及无穷级数的收敛性判断等核心知识。还探讨了优化问题和在物理、经济学中的实际应用,提供了系统的学习框架。
源码
# 高等数学
- 函数与极限
- 函数的定义
- 映射关系
- 一对一与多对一
- 复合函数
- 函数的分类
- 初等函数
- 复合函数
- 随机函数
- 极限的概念
- 左极限与右极限
- 无穷小的定义
- 极限的性质
- 极限存在的条件
- 极限运算的性质
- 无穷小与无穷大
- 夹逼定理
- 连续性
- 连续函数的定义
- 连续性的性质
- 闭区间上的连续性
- 开区间上的连续性
- 中间值定理
- 应用举例
- 极值定理
- 边界值的讨论
- 导数
- 导数的定义
- 切线的定义
- 微分的概念
- 导数的几何意义
- 函数的增减性
- 函数的极值
- 导数的计算法则
- 乘法法则
- 除法法则
- 链式法则
- 高阶导数
- 微分与导数的应用
- 物理中的自变量变化
- 洛必达法则
- 不定型的讨论
- 积分
- 不定积分与定积分
- 积分的基本定理
- 积分的几何意义
- 面积与体积的计算
- 积分计算方法
- 换元积分法
- 分部积分法
- 数值积分法
- 定积分的性质与应用
- 基本性质
- 平均值定理
- 牛顿-莱布尼茨公式
- 无穷级数
- 数列与级数的定义
- 数列的收敛判别
- 收敛与发散的概念
- 常见级数的收敛性判断
- 比较测试
- 比率测试
- 根测试
- 辛普森测试
- 幅度级数
- 傅里叶级数
- 多变量微积分
- 多元函数的极限与连续性
- 多元极限的计算
- 偏导数与全微分
- 逐变量求导
- 多重积分及其应用
- 二重积分
- 三重积分
- 级数的润滑
- 方向导数与梯度
- 微分方程
- 常微分方程的基本概念
- 线性与非线性
- 一阶微分方程的解法
- 可分离变量法
- 齐次方程
- 线性方程
- 高阶微分方程的解法
- 常系数线性方程
- 线性微分方程的应用
- 物理模型
- 向量和曲线
- 向量的基本概念与运算
- 向量加法与标量乘法
- 曲线的参数表示
- 映射与参数化
- 曲面积分与曲线积分
- 格林定理
- 斯托克斯定理
- 散度定理
- 应用
- 优化问题及其求解
- 一维与多维优化
- Lagrange乘数法
- 物理中的应用
- 运动学与动力学
- 经济学中的应用
- 边际分析与效用函数
图片