电路原理核心框架及分析方法概述与应用
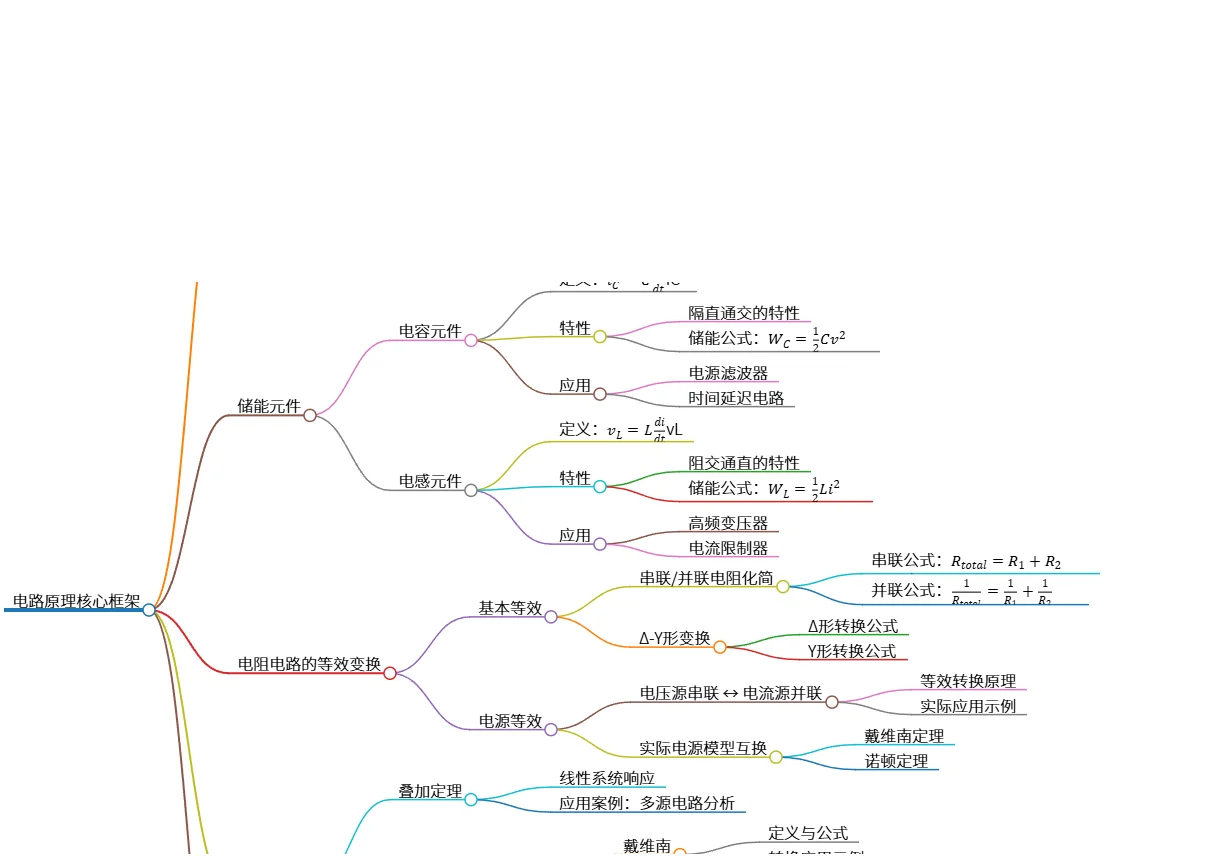
该思维导图概述了电路原理的核心框架,包括电阻电路的分析方法(KCL与KVL)、储能元件(电容和电感)、电路的等效变换(串联/并联及源等效)以及重要的电路定理(叠加、戴维南与诺顿最大功率传输定理)。此外,还介绍了动态电路分析基础,重点是RC和RL电路的一阶响应及时间常数的影响。这些内容构成了电路分析与设计的基础。
源码
# 电路原理核心框架
- 电阻电路的一般分析方法
- KCL与KVL基础
- 基尔霍夫电流定律(KCL)
- 定义:节点电流总和为零
- 应用示例:电流分配
- 基尔霍夫电压定律(KVL)
- 定义:闭合回路电压总和为零
- 应用示例:电压分配
- 三大分析方法
- 支路电流法
- 优点:适合复杂电路
- 适用情况:多支路电流分析
- 网孔电流法
- 优点:减少方程数量
- 适用情况:简单闭合回路
- 节点电压法
- 优点:直接获取节点电压
- 适用情况:多节点复杂电路
- 储能元件
- 电容元件
- 定义:$i_C = C \frac{dv}{dt}$
- 特性
- 隔直通交的特性
- 储能公式:$W_C=\frac{1}{2}Cv^2$
- 应用
- 电源滤波器
- 时间延迟电路
- 电感元件
- 定义:$v_L = L \frac{di}{dt}$
- 特性
- 阻交通直的特性
- 储能公式:$W_L=\frac{1}{2}Li^2$
- 应用
- 高频变压器
- 电流限制器
- 电阻电路的等效变换
- 基本等效
- 串联/并联电阻化简
- 串联公式:$R_{total} = R_1 + R_2$
- 并联公式:$\frac{1}{R_{total}} = \frac{1}{R_1} + \frac{1}{R_2}$
- Δ-Y形变换
- Δ形转换公式
- Y形转换公式
- 电源等效
- 电压源串联 ↔ 电流源并联
- 等效转换原理
- 实际应用示例
- 实际电源模型互换
- 戴维南定理
- 诺顿定理
- 电路定理
- 叠加定理
- 线性系统响应
- 应用案例:多源电路分析
- 戴维南与诺顿定理
- 戴维南
- 定义与公式
- 转换应用示例
- 诺顿
- 定义与公式
- 转换应用示例
- 最大功率传输定理
- 提条件
- 负载$R_L = R_{eq}$时
- 实际应用
- 音频设备匹配
- 无线电发射功率优化
- 动态电路分析基础
- 一阶RC/RL电路
- 时间常数
- 计算公式:$\tau = RC$ 或 $\tau = L/R$
- 影响分析:影响电路响应速率
- 三要素法
- 公式:$f(t)=f(\infty)+[f(0_+)-f(\infty)]e^{-t/\tau}$
- 应用示例:电容充放电过程
图片