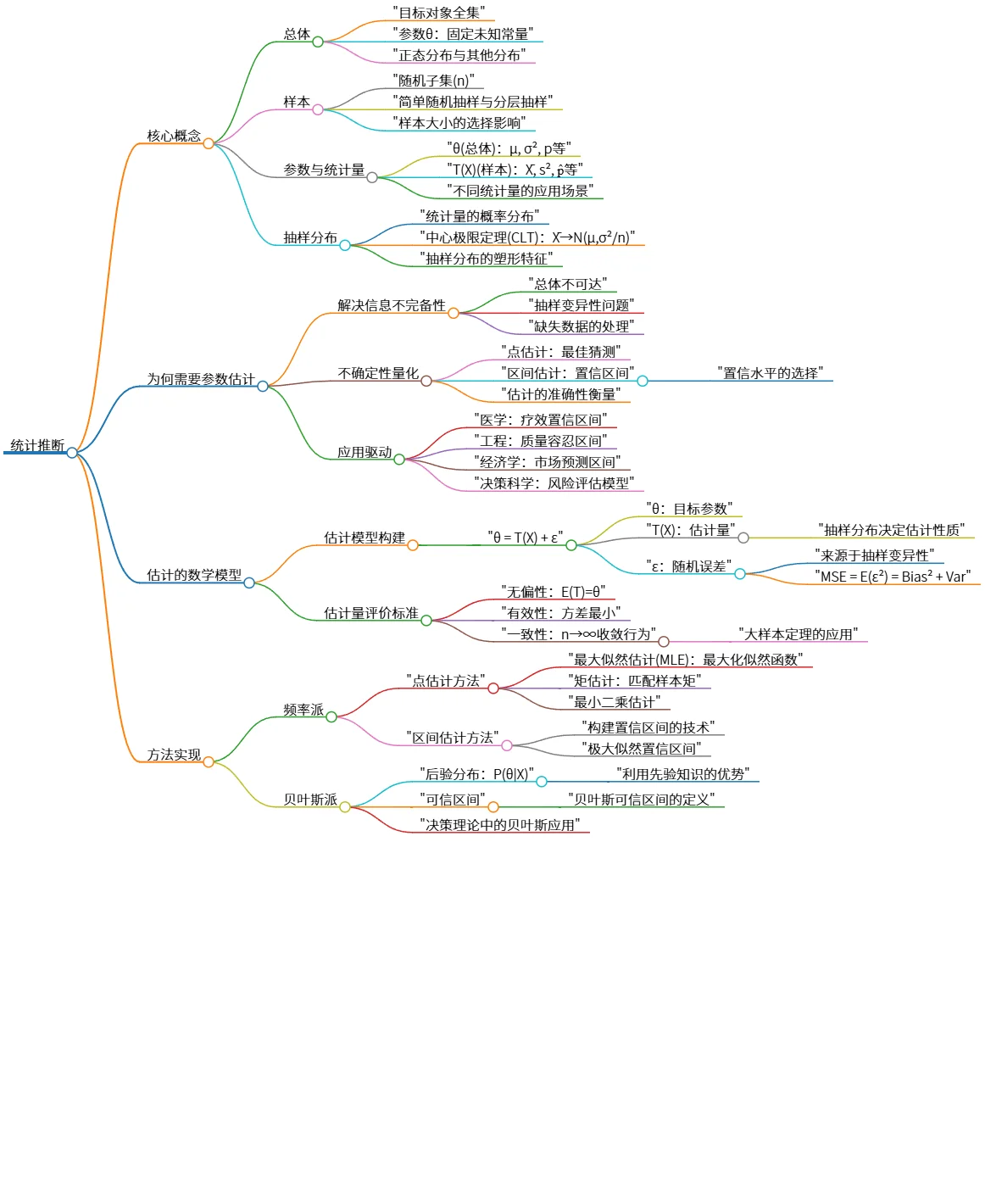
统计推断：核心概念、参数估计及方法实现探讨

# 统计推断
## 核心概念
- 总体
  - "目标对象全集"
  - "参数θ：固定未知常量"
  - "正态分布与其他分布"
- 样本
  - "随机子集(n)"
  - "简单随机抽样与分层抽样"
  - "样本大小的选择影响"
- 参数与统计量
  - "θ(总体)：μ, σ², p等"
  - "T(X)(样本)：X̄, s², p̂等"
  - "不同统计量的应用场景"
- 抽样分布
  - "统计量的概率分布"
  - "中心极限定理(CLТ)：X̄→N(μ,σ²/n)"
  - "抽样分布的塑形特征"

## 为何需要参数估计
- 解决信息不完备性
  - "总体不可达"
  - "抽样变异性问题"
  - "缺失数据的处理"
- 不确定性量化
  - "点估计：最佳猜测"
  - "区间估计：置信区间"
    - "置信水平的选择"
  - "估计的准确性衡量"
- 应用驱动
  - "医学：疗效置信区间"
  - "工程：质量容忍区间"
  - "经济学：市场预测区间"
  - "决策科学：风险评估模型"

## 估计的数学模型
- 估计模型构建
  - "θ = T(X) + ε"
    - "θ：目标参数"
    - "T(X)：估计量"
      - "抽样分布决定估计性质"
    - "ε：随机误差"
      - "来源于抽样变异性"
      - "MSE = E(ε²) = Bias² + Var"
- 估计量评价标准
  - "无偏性：E(T)=θ"
  - "有效性：方差最小"
  - "一致性：n→∞收敛行为"
    - "大样本定理的应用"

## 方法实现
- 频率派
  - "点估计方法"
    - "最大似然估计(MLE)：最大化似然函数"
    - "矩估计：匹配样本矩"
    - "最小二乘估计"
  - "区间估计方法"
    - "构建置信区间的技术"
    - "极大似然置信区间"
- 贝叶斯派
  - "后验分布：P(θ|X)"
    - "利用先验知识的优势"
  - "可信区间"
    - "贝叶斯可信区间的定义"
  - "决策理论中的贝叶斯应用"