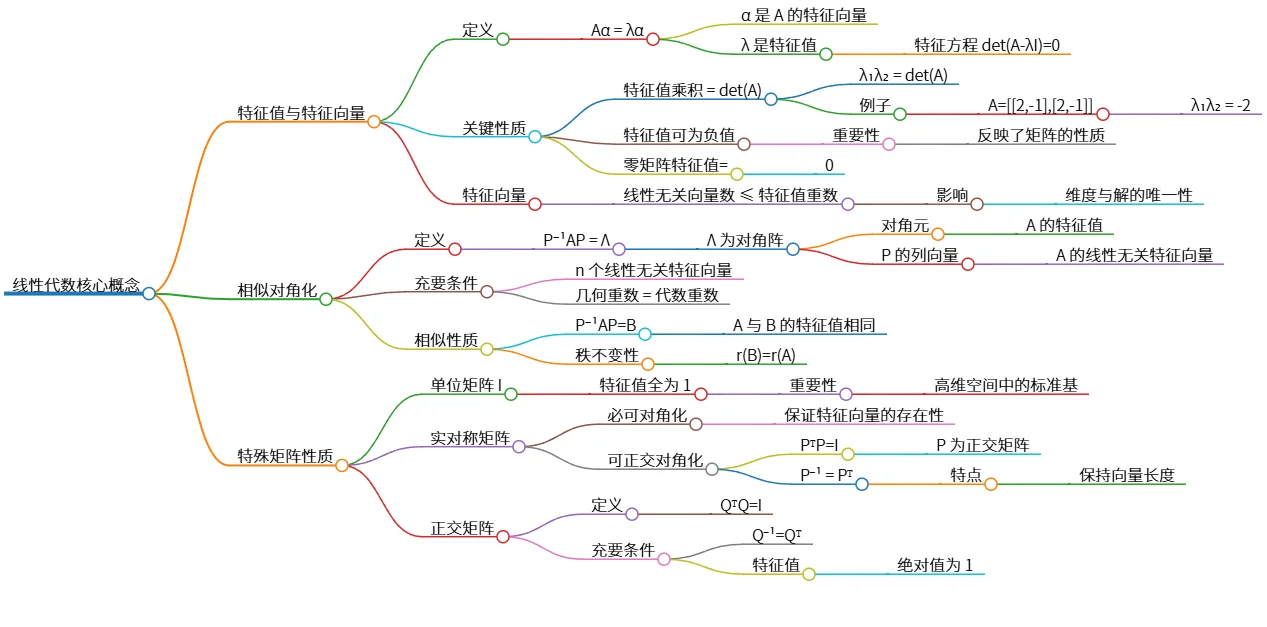
线性代数核心概念：特征值、相似对角化与特殊矩阵性质

该思维导图概述了线性代数中的核心概念，包括特征值与特征向量的定义、性质和特征方程；相似对角化的定义及其充要条件；以及特殊矩阵的性质，如单位矩阵、实对称矩阵和正交矩阵。重点强调了特征值与特征向量的关系、对角化的必要条件以及不同类型矩阵的特性及相似性质。这些概念是理解线性代数基础的重要组成部分。

源码

# 线性代数核心概念
## 特征值与特征向量
- 定义
  - Aα = λα
    - α 是 A 的特征向量
    - λ 是特征值
      - 特征方程 det(A-λI)=0
- 关键性质
  - 特征值乘积 = det(A)
    - λ₁λ₂ = det(A)
    - 例子
      - A=[[2,-1],[2,-1]]
        - λ₁λ₂ = -2
  - 特征值可为负值
    - 重要性
      - 反映了矩阵的性质
  - 零矩阵特征值=
    - 0
- 特征向量
  - 线性无关向量数 ≤ 特征值重数
    - 影响
      - 维度与解的唯一性

## 相似对角化
- 定义
  - P⁻¹AP = Λ
    - Λ 为对角阵
      - 对角元
        - A 的特征值
      - P 的列向量
        - A 的线性无关特征向量
- 充要条件
  - n 个线性无关特征向量
  - 几何重数 = 代数重数
- 相似性质
  - P⁻¹AP=B
    - A 与 B 的特征值相同
  - 秩不变性
    - r(B)=r(A)

## 特殊矩阵性质
- 单位矩阵 I
  - 特征值全为 1
    - 重要性
      - 高维空间中的标准基
- 实对称矩阵
  - 必可对角化
    - 保证特征向量的存在性
  - 可正交对角化
    - PᵀP=I
      - P 为正交矩阵
    - P⁻¹ = Pᵀ
      - 特点
        - 保持向量长度
- 正交矩阵
  - 定义
    - QᵀQ=I
  - 充要条件
    - Q⁻¹=Qᵀ
    - 特征值
      - 绝对值为 1

图片