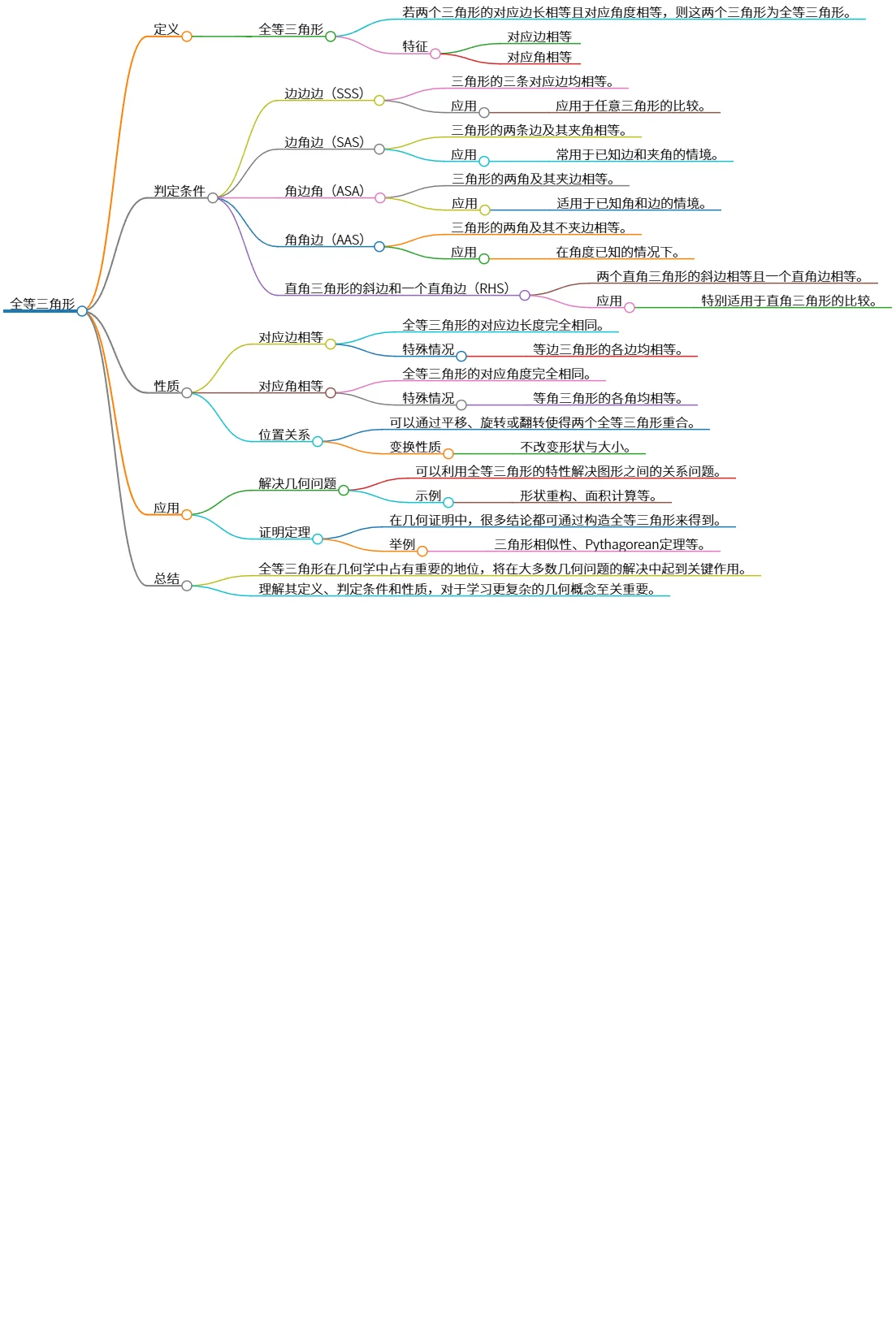
全等三角形的定义、判定条件与基本性质解析

# 全等三角形
## 定义
- 全等三角形
  - 若两个三角形的对应边长相等且对应角度相等，则这两个三角形为全等三角形。
  - 特征
    - 对应边相等
    - 对应角相等
## 判定条件
- 边边边（SSS）
  - 三角形的三条对应边均相等。
  - 应用
    - 应用于任意三角形的比较。
- 边角边（SAS）
  - 三角形的两条边及其夹角相等。
  - 应用
    - 常用于已知边和夹角的情境。
- 角边角（ASA）
  - 三角形的两角及其夹边相等。
  - 应用
    - 适用于已知角和边的情境。
- 角角边（AAS）
  - 三角形的两角及其不夹边相等。
  - 应用
    - 在角度已知的情况下。
- 直角三角形的斜边和一个直角边（RHS）
  - 两个直角三角形的斜边相等且一个直角边相等。
  - 应用
    - 特别适用于直角三角形的比较。
## 性质
- 对应边相等
  - 全等三角形的对应边长度完全相同。
  - 特殊情况
    - 等边三角形的各边均相等。
- 对应角相等
  - 全等三角形的对应角度完全相同。
  - 特殊情况
    - 等角三角形的各角均相等。
- 位置关系
  - 可以通过平移、旋转或翻转使得两个全等三角形重合。
  - 变换性质
    - 不改变形状与大小。
## 应用
- 解决几何问题
  - 可以利用全等三角形的特性解决图形之间的关系问题。
  - 示例
    - 形状重构、面积计算等。
- 证明定理
  - 在几何证明中，很多结论都可通过构造全等三角形来得到。
  - 举例
    - 三角形相似性、Pythagorean定理等。
## 总结
- 全等三角形在几何学中占有重要的地位，将在大多数几何问题的解决中起到关键作用。
- 理解其定义、判定条件和性质，对于学习更复杂的几何概念至关重要。