线性代数核心概念及方法详解
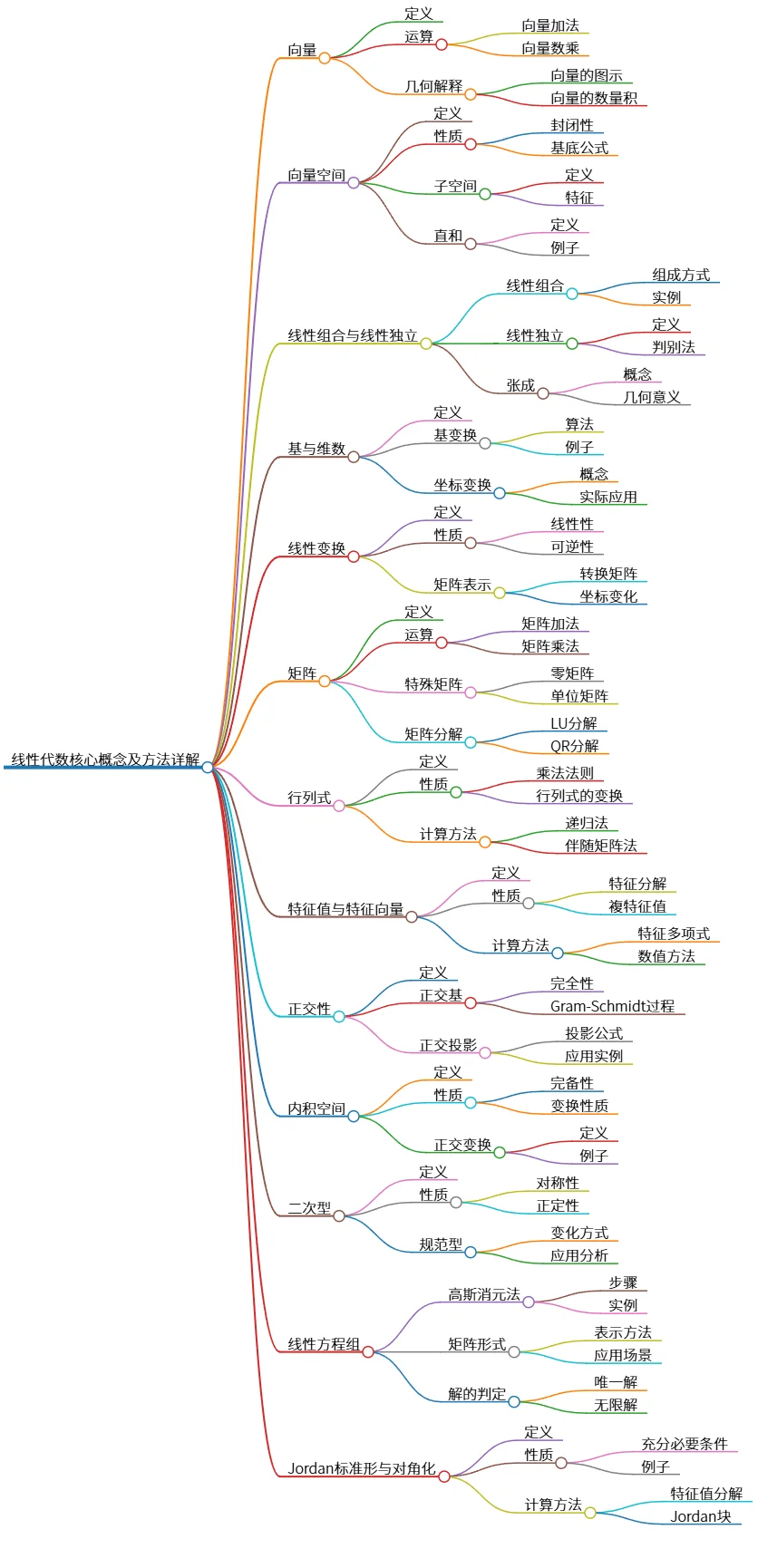
该思维导图概述了线性代数的核心概念,涵盖向量、向量空间、线性组合与线性独立、基与维数、线性变换、矩阵、行列式、特征值与特征向量、正交性、内积空间、二次型以及线性方程组和Jordan标准形与对角化等重要内容。 它系统地阐述了每个主题的定义、性质、运算及计算方法,并涵盖了其几何解释及应用,例如基变换、坐标变换、矩阵分解和高斯消元法等。 这是一个线性代数知识体系的完整框架。
源码
# 线性代数核心概念及方法详解
## 向量
### 定义
### 运算
#### 向量加法
#### 向量数乘
### 几何解释
#### 向量的图示
#### 向量的数量积
## 向量空间
### 定义
### 性质
#### 封闭性
#### 基底公式
### 子空间
#### 定义
#### 特征
### 直和
#### 定义
#### 例子
## 线性组合与线性独立
### 线性组合
#### 组成方式
#### 实例
### 线性独立
#### 定义
#### 判别法
### 张成
#### 概念
#### 几何意义
## 基与维数
### 定义
### 基变换
#### 算法
#### 例子
### 坐标变换
#### 概念
#### 实际应用
## 线性变换
### 定义
### 性质
#### 线性性
#### 可逆性
### 矩阵表示
#### 转换矩阵
#### 坐标变化
## 矩阵
### 定义
### 运算
#### 矩阵加法
#### 矩阵乘法
### 特殊矩阵
#### 零矩阵
#### 单位矩阵
### 矩阵分解
#### LU分解
#### QR分解
## 行列式
### 定义
### 性质
#### 乘法法则
#### 行列式的变换
### 计算方法
#### 递归法
#### 伴随矩阵法
## 特征值与特征向量
### 定义
### 性质
#### 特征分解
#### 複特征值
### 计算方法
#### 特征多项式
#### 数值方法
## 正交性
### 定义
### 正交基
#### 完全性
#### Gram-Schmidt过程
### 正交投影
#### 投影公式
#### 应用实例
## 内积空间
### 定义
### 性质
#### 完备性
#### 变换性质
### 正交变换
#### 定义
#### 例子
## 二次型
### 定义
### 性质
#### 对称性
#### 正定性
### 规范型
#### 变化方式
#### 应用分析
## 线性方程组
### 高斯消元法
#### 步骤
#### 实例
### 矩阵形式
#### 表示方法
#### 应用场景
### 解的判定
#### 唯一解
#### 无限解
## Jordan标准形与对角化
### 定义
### 性质
#### 充分必要条件
#### 例子
### 计算方法
#### 特征值分解
#### Jordan块
图片