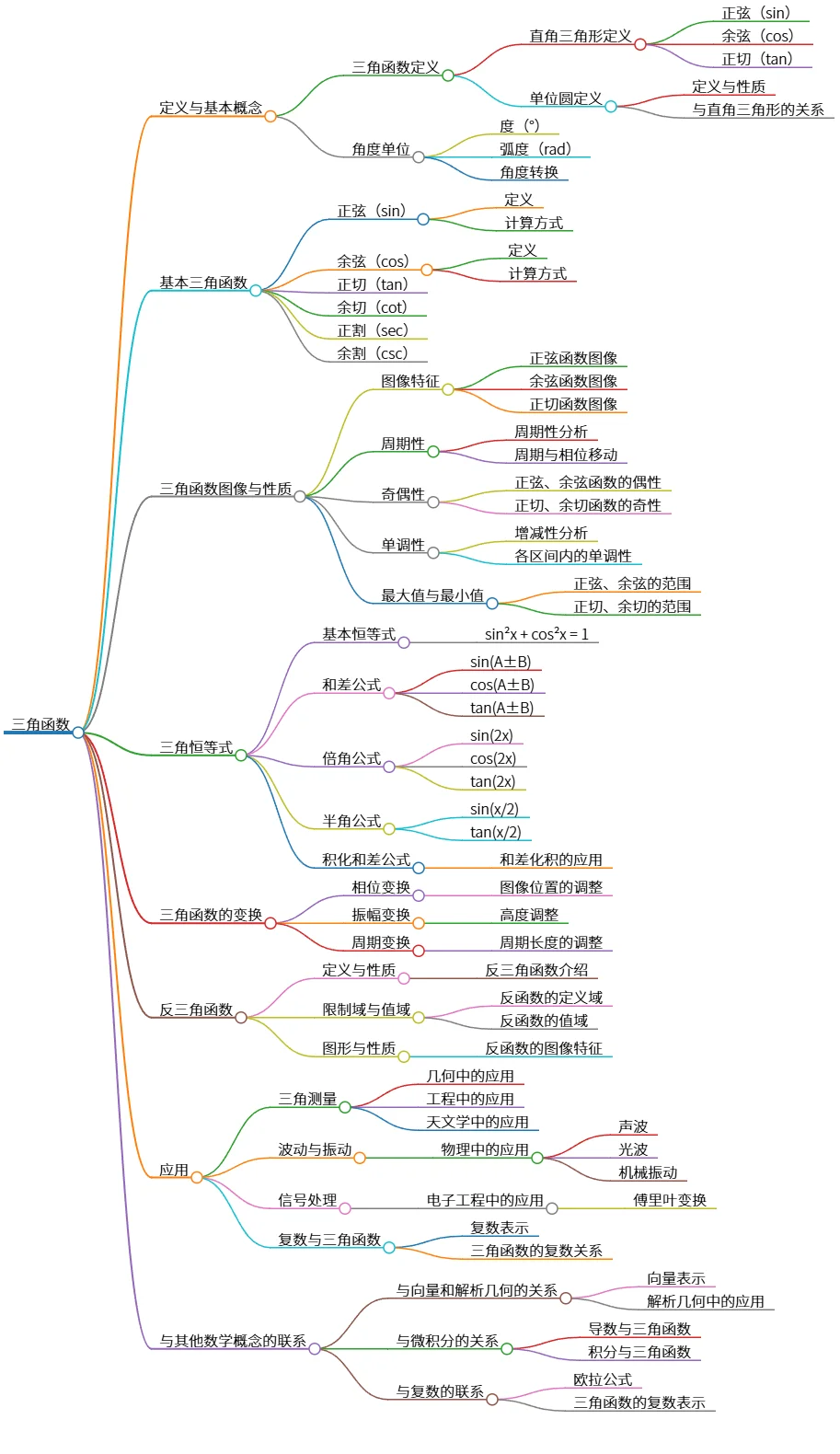
三角函数：定义、性质、恒等式及应用

# 三角函数
## 定义与基本概念
### 三角函数定义
- 直角三角形定义
  - 正弦（sin）
  - 余弦（cos）
  - 正切（tan）
- 单位圆定义
  - 定义与性质
  - 与直角三角形的关系
### 角度单位
- 度（°）
- 弧度（rad）
- 角度转换
## 基本三角函数
- 正弦（sin）
  - 定义
  - 计算方式
- 余弦（cos）
  - 定义
  - 计算方式
- 正切（tan）
- 余切（cot）
- 正割（sec）
- 余割（csc）
## 三角函数图像与性质
### 图像特征
- 正弦函数图像
- 余弦函数图像
- 正切函数图像
### 周期性
- 周期性分析
- 周期与相位移动
### 奇偶性
- 正弦、余弦函数的偶性
- 正切、余切函数的奇性
### 单调性
- 增减性分析
- 各区间内的单调性
### 最大值与最小值
- 正弦、余弦的范围
- 正切、余切的范围
## 三角恒等式
### 基本恒等式
- sin²x + cos²x = 1
### 和差公式
- sin(A±B)
- cos(A±B)
- tan(A±B)
### 倍角公式
- sin(2x)
- cos(2x)
- tan(2x)
### 半角公式
- sin(x/2)
- tan(x/2)
### 积化和差公式
- 和差化积的应用
## 三角函数的变换
### 相位变换
- 图像位置的调整
### 振幅变换
- 高度调整
### 周期变换
- 周期长度的调整
## 反三角函数
### 定义与性质
- 反三角函数介绍
### 限制域与值域
- 反函数的定义域
- 反函数的值域
### 图形与性质
- 反函数的图像特征
## 应用
### 三角测量
- 几何中的应用
- 工程中的应用
- 天文学中的应用
### 波动与振动
- 物理中的应用
  - 声波
  - 光波
  - 机械振动
### 信号处理
- 电子工程中的应用
  - 傅里叶变换
### 复数与三角函数
- 复数表示
- 三角函数的复数关系
## 与其他数学概念的联系
### 与向量和解析几何的关系
- 向量表示
- 解析几何中的应用
### 与微积分的关系
- 导数与三角函数
- 积分与三角函数
### 与复数的联系
- 欧拉公式
- 三角函数的复数表示